回溯法操作

回溯法操作是一種滿足一定約束條件的優選搜尋法，該方法的搜尋通過一個多階段的確定過程來實現；在每一階段都需要從一些選擇中選擇一個分支，一旦發現前面的選擇不可能獲得一個解，則算法進行回溯，即重新回到剛搜尋過的選擇點，並選擇該結點另一個沒有被試過的分支；如果該點處所有的分支都已試過，則算法回溯到該結點之前被選擇的點，而滿足回溯條件的這個狀態點就稱為回溯點。

基本介紹

• 中文名：回溯法操作
• 外文名：Backtracking operation
• 學科：計算機科學與技術
• 美譽：通用解題法
• 別名：試探法
• 基本行為：搜尋

基本思想

回溯法也稱為試探法，該方法的基本思想是：從一條路往前走，能進則進，不能進則退，換一條路再試，直到所有的路徑都試到。它的求解過程實質上是一個先根遍歷一棵“狀態空間樹”的過程，只是這棵樹不是遍歷前預先建立的，而是隱含在遍歷過程中的。當試探過程中出現的狀態和問題所求解產生矛盾時，不再繼續試探下去，這時出現的葉子結點不是問題的解的終結狀態。這類問題的求解過程可看成是在約束條件下進行先根遍歷，並在遍歷過程中剪去那些不滿足條件的分支。為了套用回溯法，所要求的解必須能表示成一組約束條件，通常要求所有的解滿足一組綜合的約束條件。

多約束條件下的合理分配問題在網路規劃、模式識別及多目標最佳化等眾多領域有著廣泛的套用。這些問題往往涉及多個約束的同時最佳化，但各約束間常存在衝突，因此尋求多約束條件下的合理分配問題的最優解或可接受解一直是數學及計算機領域中重要的研究課題。回溯法是解決聯合搜尋問題的一個重要方法，算法的基本策略之一，是在問題的解空間中，按照深度優先的策略從根結點出發搜尋解空間樹，在搜尋的過程中，根據實際問題的基本要求和最佳化規則，確定相應的選優條件和優先權，由此對解空間進行剪枝，以提高搜尋速度，得到最優解或可接受解。

操作思路

簡單描述

回溯法思路的簡單描述是：把問題的解空間轉化成了圖或者樹的結構表示，然後使用深度優先搜尋策略進行遍歷，遍歷的過程中記錄和尋找所有可行解或者最優解。基本思想類同於：圖的深度優先搜尋和二叉樹的後序遍歷。當問題是要求滿足某種性質（約束條件）的所有解或最優解時，往往使用回溯法。它有“通用解題法”之美譽。

詳細描述

詳細的描述則為：回溯法按深度優先策略搜尋問題的解空間樹。首先從根節點出發搜尋解空間樹，當算法搜尋至解空間樹的某一節點時，先利用剪枝函式判斷該節點是否可行（即能得到問題的解）。如果不可行，則跳過對該節點為根的子樹的搜尋，逐層向其祖先節點回溯；否則，進入該子樹，繼續按深度優先策略搜尋。

回溯法的基本行為是搜尋，搜尋過程使用剪枝函式來為了避免無效的搜尋。剪枝函式包括兩類：

（1）使用約束函式，剪去不滿足約束條件的路徑；

（2）使用限界函式，剪去不能得到最優解的路徑。

問題的關鍵在於如何定義問題的解空間，轉化成樹（即解空間樹）。解空間樹分為兩種：子集樹和排列樹。兩種在算法結構和思路上大體相同。

實現方法

回溯法的實現方法有兩種：遞歸和遞推（也稱疊代）。一般來說，一個問題兩種方法都可以實現，只是在算法效率和設計複雜度上有區別。

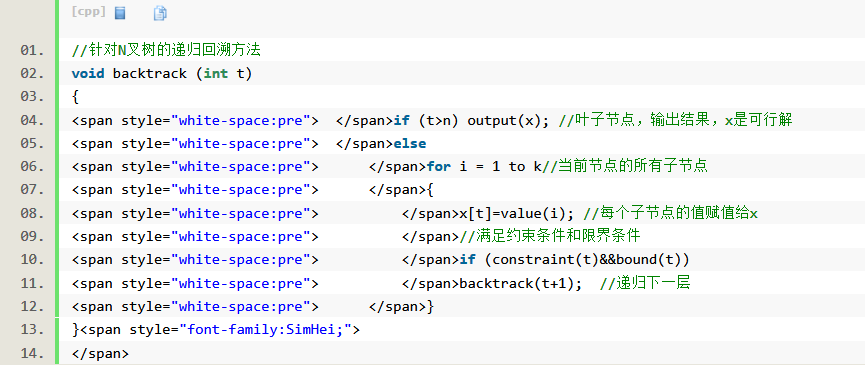
遞歸

思路簡單，設計容易，但效率低，其設計範式如下：

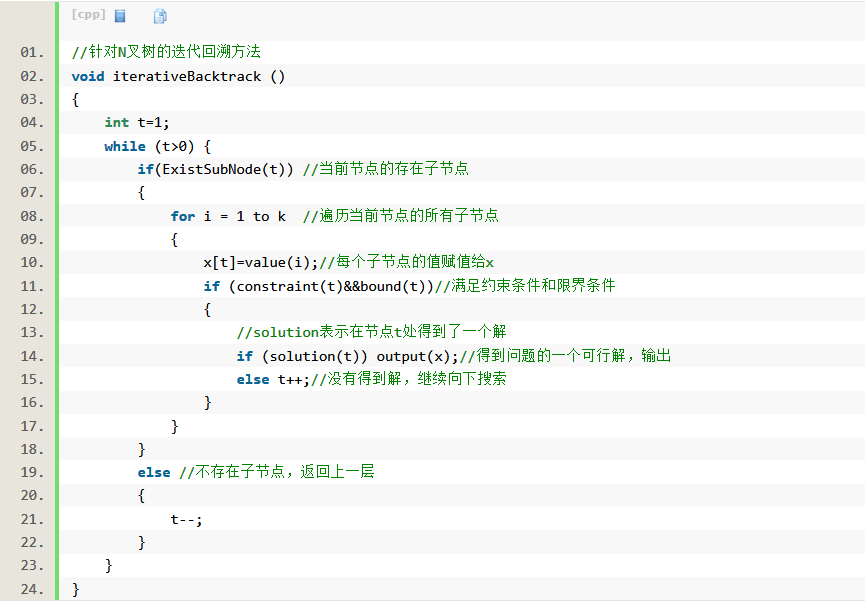
遞推

算法設計相對複雜，但效率高。其設計範式如下：

算法分類

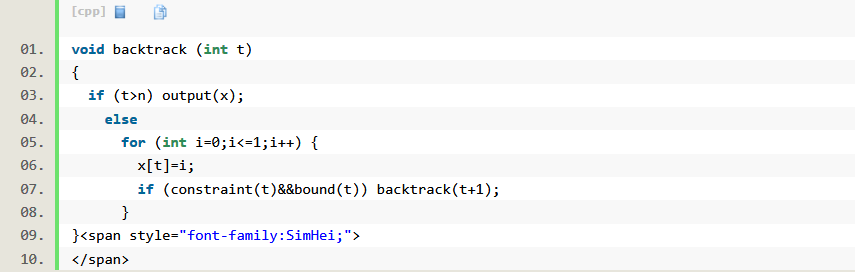
子集樹

所給的問題是從n個元素的集合S中找出滿足某種性質的子集時，相應的解空間成為子集樹。

如0-1背包問題，從所給重量、價值不同的物品中挑選幾個物品放入背包，使得在滿足背包不超重的情況下，背包內物品價值最大。它的解空間就是一個典型的子集樹。

回溯法搜尋子集樹的算法範式如下：

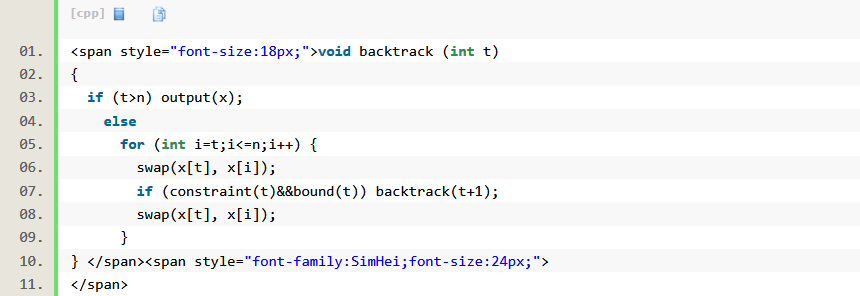
排列樹

所給的問題是確定n個元素滿足某種性質的排列時，相應的解空間就是排列樹。

如旅行售貨員問題，一個售貨員把幾個城市旅行一遍，要求走的路程最小。它的解就是幾個城市的排列，解空間就是排列樹。

回溯法搜尋排列樹的算法範式如下：

實例套用

利用回溯法解決問題的幾個經典問題如下：

（1）裝載問題

（2）0-1背包問題

（3）旅行售貨員問題

（4）八皇后問題

（5）迷宮問題

（6）圖的m著色問題

（7）宿舍分配問題

0-1背包問題

問題：給定n種物品和一背包。物品i的重量是wi，其價值為pi，背包的容量為C。問應如何選擇裝入背包的物品，使得裝入背包中物品的總價值最大?

分析：問題是n個物品中選擇部分物品，可知，問題的解空間是子集樹。比如物品數目n=3時，其解空間樹如下圖1，邊為1代表選擇該物品，邊為0代表不選擇該物品。使用x[i]表示物品i是否放入背包，x[i]=0表示不放，x[i]=1表示放入。回溯搜尋過程，如果來到了葉子節點，表示一條搜尋路徑結束，如果該路徑上存在更優的解，則保存下來。如果不是葉子節點，是中點的節點（如B），就遍歷其子節點（D和E），如果子節點滿足剪枝條件，就繼續回溯搜尋子節點。

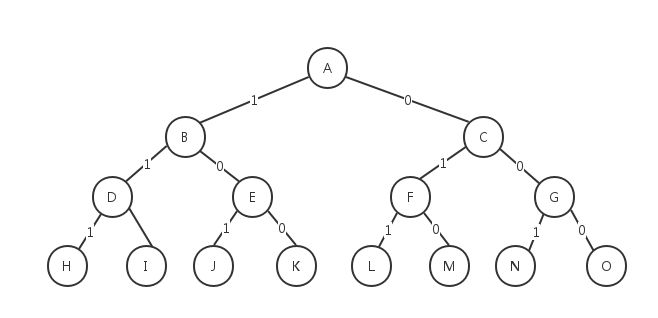
圖1

學生宿舍分配問題

學生宿舍分配問題，其簡化數學模型可概括為一個資源分配模型，即將某種定量資源分配給不同的需求個體， 同時滿足一定的約束條件。具體講，學生宿舍分配就是按一定的分配方法，根據學生的基本特徵，分配合適的宿舍。作為資源分配模型的實例，學生宿舍分配問題應符合下面幾個基本要求 ：

（1）需求集:需求集合中包含的元素個數是有限的;每個元素具有一系列特徵；正是這些特徵使不同的需求個體相互區別；對於學生宿舍分配問題而言，需求集就是某一類需要分配宿舍的學生集合，其特徵有姓名、性別、成績、來源地等；

（2）資源集：資源的總數是有限的， 不同資源是可以區分的；對於學生宿舍分配問題而言， 資源集合中的元素就是學生公寓的房間，其特徵有所在樓號、所在層數、應住人數、實住人數、宿舍類別等；

（3）約束條件群：需求集中的元素特徵與資源集中的元素特徵相互作用形成的數學關係，構成了約束條件群。對於學生宿舍分配問題而言，最主要的約束條件是：每個公寓房間可以對應若干個學生， 但一個學生只能對應一個房間；在此基礎上，還可以依據一定的特徵定義其它軟約束， 如：同一班級的所有宿舍,，學生的學習情況儘可能均衡；同一宿舍的學生儘可能來源地不同等等；

（4）解集：符契約束條件的一組解， 實質就是需求集與資源集之間的對應關係，也就是宿舍分配結果。

學生宿舍分配的基本要求與任務就是為每個在校生選擇一個宿舍。此外，在論證學生個體之間及與宿舍集體之間的關係和相互影響的基礎上， 在學校條件允許的前提下，遵從科學化、合理化、人性化的原則， 還應該依據下列因素對學生宿舍分配方法進行最佳化：

（1）不同宿舍學生的學習情況儘可能均衡；

（2）同一宿舍的學生儘可能來源地不同；

（3）同一院系、年級、專業、班級的男生或女生， 住宿儘可能集中；

（4）提供不同的宿舍類別供學生選擇。

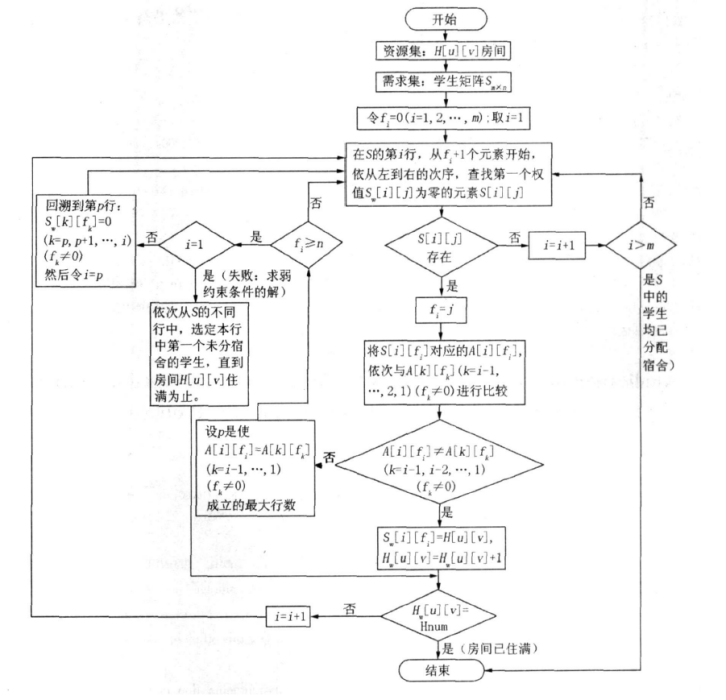
以上基本要求和最佳化規則就是學生分配宿舍問題的約束條件群，也是分配問題過程中的選優條件；這些宿舍分配的基本要求和最佳化規則，其優先權是遞減的；如果在分配過程中不滿足約束條件群， 該選擇即為不優或達不到目標；當遍歷該步驟的所有可能仍未滿足約束條件群，該狀態就滿足了回溯條件，則從該回溯點退回去重新選擇，這就是宿舍分配問題回溯算法的基本思想。其操作步驟如下圖2：

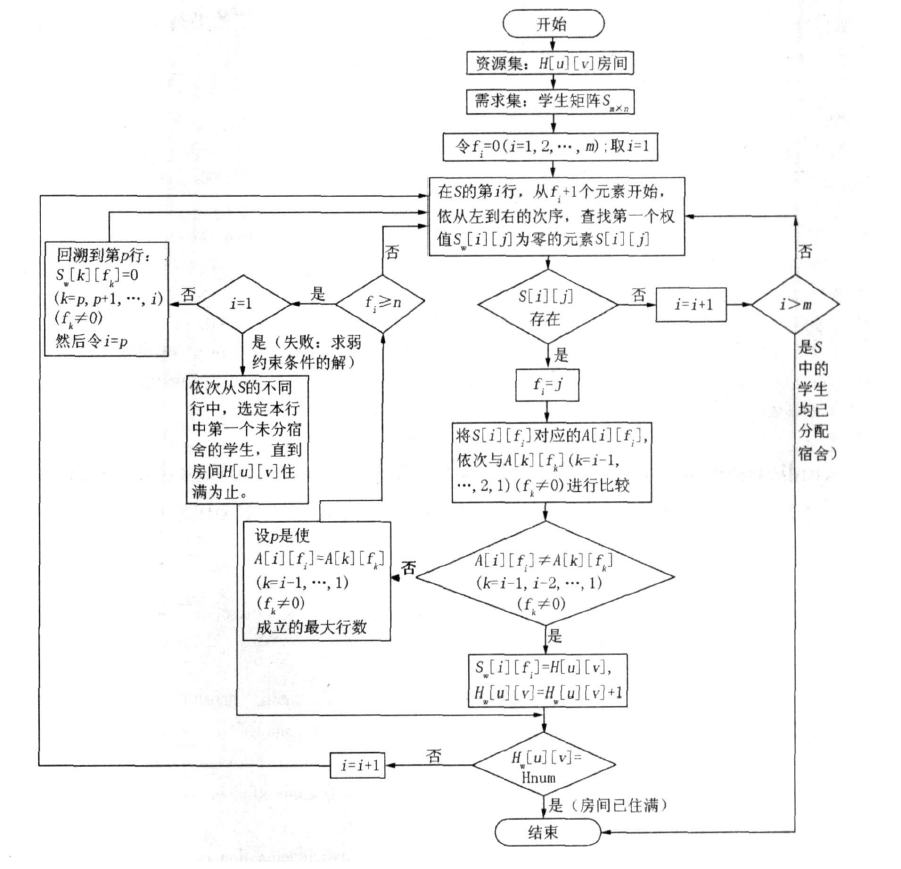
圖2