分析多變數控制系統穩定性能和動態性能的一種重要工具,多變數系統的穩定性能和動態性能等都與相應的回比矩陣密切相關。與之相關的還有回差矩陣。
基本介紹
- 中文名:回比矩陣
- 外文名:return-ratio matrix
- 定義:分析多變數控制的工具
- 意義:與多變數系統的穩定性等密切相關
- 相關概念:回差矩陣
- 所屬學科 :信息科學
簡介,定義,
簡介
分析多變數控制系統穩定性能和動態性能的一種重要工具,多變數系統的穩定性能和動態性能等都與相應的回比矩陣密切相關。與之相關的還有回差矩陣。回差矩陣也是分析多變數控制系統穩定性能和動態性能的一種重要工具,多變數系統的穩定性和整體性等都與相應的回差矩陣密切相關。
定義
在下圖所示的多變數控制系統中,v為輸入向量,e為誤差向量,u為控制向量,y0為對象輸出向量,y為系統輸出向量,G(s)為被控制對象的傳遞函式矩陣,K(s)和L(s)分別為控制器和輸出補償器的傳遞函式矩陣,F(s)為感測器的傳遞函式矩陣。
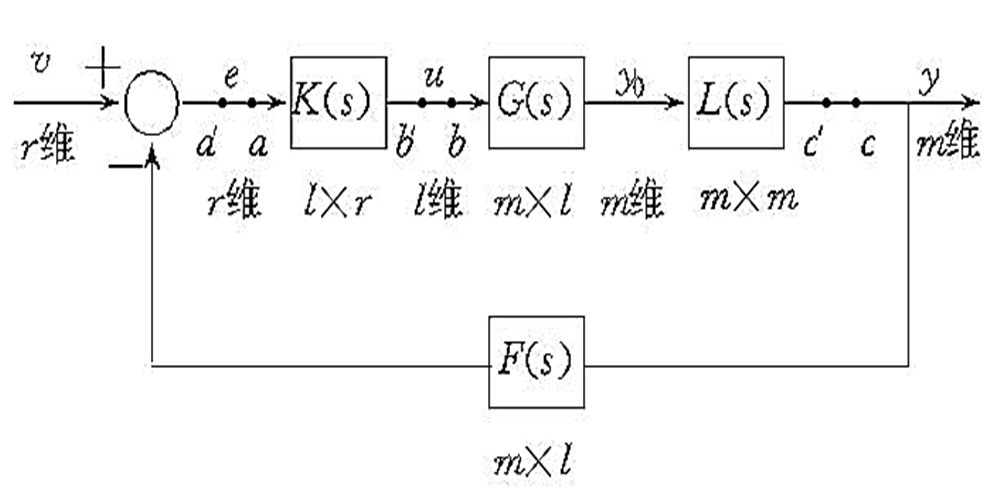
若在a′~a之間斷開閉環,並在a點加入信號,而在a′點取出信號,則從a點沿迴路到a′點的傳遞函式矩陣反號後定義為該系統關於a點的回比矩陣,記為

回比矩陣相當於單變數控制系統的開環傳遞函式,但回比矩陣(及其維數)因斷點位置不同而不同.若在b′~b之間斷開閉環,則仿上可定義該系統關於b點的回比矩陣為
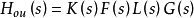

多變數系統的穩定性能和動態性能等都與相應的回比矩陣密切相關。

