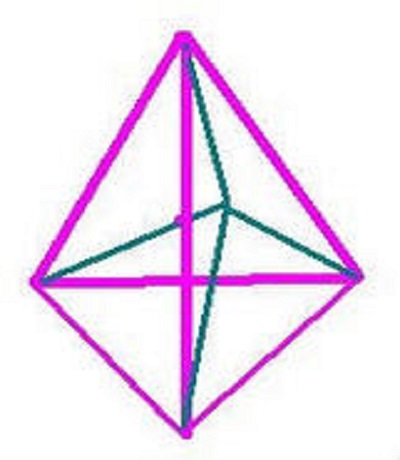
四維四面體(又稱超四面體)是由5個在不同空間的點互相連線而成的。
基本介紹
- 中文名:四維四面體
- 定義:5個在不同空間的點互相連線
- 包括:5個點10條線
- 投影:不同角度的四維四面體
簡介,三維投影,推理過程,通過坐標系推理,通過數點法推理,
簡介
形狀
四維四面體(超四面體)中包括:
5個點
10條線
5個四面體
三維投影
這裡是不同角度的四維四面體(超四面體)在不同角度下的三維投影
注釋:這是在一個四面體外(內)任意確定 一個點分別向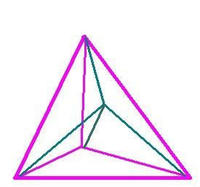
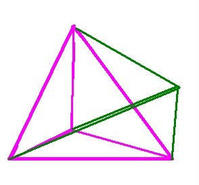
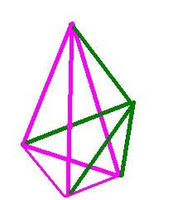



原四面體的四個點連線而成的。
推理過程
通過坐標系推理
三維的坐標系是三條相互垂直的直線,但它在平面中的投影有一條線是不與另外兩條垂直的。 那么根據定義,四維空間中的坐標系是四條互相垂直的直線構成的(不在同一空間中),那么 根據推理它在三維中的投影也應有一條線不與另外三條垂直。
如果把二維坐標系中的四個點,每三個點都連成一個三角形便得到了三維四面體在二維中的投影
那么同理如果把三維坐標系中的五個點,每四個點都連成一個四面體便得到了四維四面體(超四面體)在維中的投影
通過數點法推理
一維最基本的圖形是線,是由兩個點相互連線而成的.
二維最基本的圖形是三角形,是由三個點互相連線而成的。
三維最基本的圖形是四面體,是由四個 不在同一平面 上的點互相連線而成的。但它在二維中的投影是在 在同一平面 上的四個點互相連線而成的。
同理,四維最基本的圖形是四維四面體 (超四面體) 是五個 不在同一空間 上的五個點互相連線而成的。但它在三維中的投影是在 在同一空間 上的五個點互相連線而成的。
由此就得到了四維四面體(超四面體)在三維中的投影.