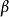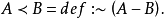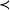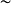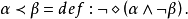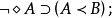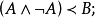嚴格蘊涵(strict implication)是蘊涵的一種，用於模態邏輯。它最初由英國邏輯學家麥柯爾(H.MacColl)提出，美國哲學家、邏輯學家劉易斯劉易斯(C.I.Lewis)在創立現代模態邏輯時使用了這種蘊涵。嚴格蘊涵用魚鉤符號“⊰”表示，它可以由模態運算元◇(稱為“可能運算元”，◇p意為“p是可能的”)或□(稱為“必然運算元”，□p意為“p是必然的”)以及真值聯結詞來定義。在劉易斯的模態邏輯系統中，A⊰B(讀作“A嚴格蘊涵B”)被定義為¬◇(A∧¬B)(讀作“‘A真且B假’是不可能的”)。A⊰B也可以被等價地定義為□(A→B)(讀作“‘A實質蘊涵B’是必然的”)。“A實質蘊涵B”只意味著“A真而B假”，這個命題是假命題。當命題A與命題B之間存在某種必然聯繫時，即A真而B假為不可能時，稱A“嚴格蘊涵”B。日常語言中的“蘊涵”所指的就是嚴格蘊涵。
基本介紹
- 中文名：嚴格蘊涵
- 外文名：strict implication;tautological implication
- 所屬學科：數學
- 所屬問題：現代邏輯(非經典邏輯)
- 相關人物：麥柯爾、劉易斯等
- 相關概念：模態命題邏輯，實質蘊涵等
基本介紹,針對問題,嚴格蘊涵的定義,性質及舉例,起源及相關研究,
基本介紹
針對問題
在命題邏輯中，我們將“如果P那么Q”符號為“P→Q”。“P→Q”叫做“實質蘊涵”。實質蘊涵的邏輯性質完全由“→”的特徵真值表決定。一個明顯的事實是，“→”與日常語言的“如果…那么…”的含義並不完全相同，有時相去甚遠。例如：
(1)李白是詩人→2+2=4
是一個真命題，既然它的前件和後件都是真的。但是
(2)如果李白是詩人，那么2+2=4
在日常語言中則是一個假命題甚至是無意義的。這是因為日常語言中的蘊涵命題的真值不僅取決於前件和後件的真值，而且取決於前件和後件之間的關係。具體地說，僅當前件和後件之間具有某種必然聯繫時，日常語言中的蘊涵命題才為真。命題(2)之所以常常被人們看作假的，就是因為它的前件和後件之間沒有必然聯繫。
嚴格蘊涵的定義
模態命題邏輯的一個重要目標是要較好地反映日常語言的蘊涵命題。為了做到這一點，模態命題邏輯提出一種不同於實質蘊涵的蘊涵關係，即“嚴格蘊涵”，其定義是：
P嚴格蘊涵Q，若且唯若，P→Q是必然的。
性質及舉例
從這個定義我們可以看出，嚴格蘊涵命題比實質蘊涵命題斷定得更多更強。因此，如果一個命題作為嚴格蘊涵命題是真的，那么，該命題作為實質蘊涵命題也是真的；換言之，如果一個命題作為實質蘊涵命題是假的，那么，該命題作為嚴格蘊涵命題也是假的，請注意，此論斷的逆論斷不成立。我們考察幾個具體的例子。
(3)如果3被2整除，那么9被2整除。
(4)如果美國有核武器，那么美國立即發動第三次世界大戰。
(3)作為嚴格蘊涵命題是真的。因為它的前件和後件之間的蘊涵關係具有必然性；(3)作為實質蘊涵命題也是真的，既然它的前件是假的。(4)作為實質蘊涵命題是假的，因為(4)的前件真而後件假；同時，(4)的前件真而後件假這一事實足以表明(4)的前件和後件之間沒有必然聯繫，因而(4)作為嚴格蘊涵命題也是假的。
(5)如果太陽從東邊升起，那么雪是白的。
(6)如果太陽從東邊升起，那么早晨東方先亮。
(5)和(6)的前件和後件都是真的，因而它們作為實質蘊涵命題都是真的；但是，作為嚴格蘊涵命題，只有(6)是真的，而(5)是假的，既然(5)的前件和後件之間沒有必然聯繫。
總之，如果一個蘊涵命題的前件真而後件假，那么該命題無論作為實質蘊涵命題還作為嚴格蘊涵命題都是假的。如果一個蘊涵命題並非前件真而後件假，那么該命題作為實質蘊涵命題是真的；但作為嚴格蘊涵命題則可能真也可能假，這取決於前件和後件之間有無必然聯繫：若有則真，若無則假。應該說，比起實質蘊涵命題，嚴格蘊涵命題更接近於日常語言的蘊涵命題。
起源及相關研究
麥柯爾(H.MacColl)早在1880年就提出了適合於刻畫嚴格條件句的新蘊涵詞，並採用符號“：”來表示，它的解釋是“如果在它前面的那個命題是真的，那么，在它後面的那個命題必然是真的”。這就是後來所說的嚴格蘊涵。麥柯爾在1903年的論文《符號推理》中，更明確說明了他的新蘊涵(：)與舊蘊涵詞(<，實質蘊涵)的聯繫及其不同涵義。
[
真，同時
假]這是不可能的。
然而，只有當美國邏輯學家劉易斯(C.I.Lewis)重新發現嚴格蘊涵之後才引起人們對它的真正注意。劉易斯的最初目的是反對他認為是錯誤的蘊涵解釋(“實質”蘊涵錯誤地暗示前後件之間的意義联系，因而引起悖論)。為了強化原來的蘊涵，在1921年的論文《蘊涵與邏輯代數》中，他對嚴格蘊涵作了如下定義：
讀作：A嚴格蘊涵B定義為不可能A而且非B。其中魚鉤符號
表示嚴格蘊涵，
表示不可能，
表示否定。如果改用現代方式，採用“可能”運算元
重新表述，那么就有：
劉易斯引進嚴格蘊涵之後，很自然地著力於建構相應的嚴格蘊涵形式系統，也就是模態命題邏輯。1932年他在與朗福德(C.H. Langford)合寫的《符號邏輯》一書中創立了模態命題邏輯S1～S5系統。可見嚴格蘊涵與模態邏輯的產生是分不開的。在邏輯哲學中蘊涵詞的演化與構造模態、相干邏輯的哲學動機實質上是同一個問題的不同側面。一般地，新算
子、新聯詞總是跟新的非經典邏輯聯繫在一起的。
嚴格蘊涵與實質蘊涵之間存在性質上的區別，實質蘊涵所刻畫的是命題之間抽象的真假關係，也就是真值函項關係(請注意：絕不是什麼內容上的具體關係)，而劉易斯用嚴格蘊涵想要刻畫的則是命題之間的邏輯關係。用
想要斷定的是B已暗含在A中，從A推出B在邏輯上是必然的，想要表示B是A的邏輯後承。但嚴格蘊涵並沒有達到劉易斯想要達到的理想境界，不過與實質蘊涵相比確實進了一大步，要求更嚴格了。實質蘊涵要求確實不是前件真而後件假，而嚴格蘊涵則要求根本不可能前件真而後件假。嚴格蘊涵系統確實避免了與前述實質蘊涵悖論相對應的命題。
儘管如此，劉易斯本人也注意到，它卻會產生新的獨特的悖論或怪論——“嚴格蘊涵悖論”，如：
(1)
(2)
(3)
(4)
。
(1)式讀作如果必然A，那么任意B嚴格蘊涵A；(2)式讀作如果不可能A，那么A嚴格蘊涵任意B；(3)式表示矛盾命題嚴格蘊涵任意命題；(4)式意即任意命題嚴格蘊涵邏輯真。劉易斯認定，儘管這些論斷與日常習慣用法極不一致，然而這些公式在邏輯上卻都是有效的，因為每一步都是無可非議的(從經典邏輯立場看確實如此)，所以他認為“怪論不怪”。這就引起了許多哲學上的爭論。
