模態運算元(modal operator)亦稱“模態詞”。 在真值模態邏輯中主要指“必 然” (可用符號□表示)和“可 能” (可用符號◇表示)。更廣義地說,模態運算元還可以包括允許、必須、禁止、相信、知道,等等。一切含有模態詞的命題就構成模態命題。在模態邏輯里研究的是建立推理的結構和規律, 構成這些推理的有含下述邏輯常項的命題,這 些邏輯常項通常用“ 必然"、“ 可能”、“ 必須”、“曾經”等,以及“能夠”、“ 允許”、“ 禁止”.“ 知 道”、“ 相 信”等,以及別的與它們有同樣作用的手段來表示的,這些邏輯常項稱作模態運算元, 此外, 還有“ 希望"、“ 需要”等尚未深入研究的模態運算元。
基本介紹
- 中文名:模態運算元
- 外文名:modal operator
- 所屬學科:數學
- 所屬問題:邏輯學(模態邏輯)
- 相關概念:模態邏輯,模態命題,模態推理等
- 別稱:模態詞
基本介紹,模態邏輯,發展歷程,模態邏輯介紹,模態命題,
基本介紹
‘‘運算元“指數學、邏輯和物理學中對某些變換(映射)或運算的稱呼。模態運算元是指模態邏輯中表示模態的運算元。所謂模態(modality)有時又稱模態詞,指事物和認識的必然性和可能性這樣一些性質,分為主觀模態和客觀模態,後者又叫邏輯模態。把模態命題形式化時對模態詞“必然”、“可能”等抽象化,形成為符號,它可以作用在命題變項前面,所代表的符號就是模態運算元。在模態系統中習慣上用“L”或“ ”表示“必然”,用“M”或“
”表示“必然”,用“M”或“ ”表示“可能”。其中
”表示“可能”。其中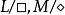 ,即為模態運算元。隨著模態邏輯的非標準化即廣義模態邏輯的發展,模態運算元的定義也擴大了,諸如時態運算元“過去P”、“將來F”、“將來總是G”、拓撲運算元P、道義運算元“應該”、“必須”、“允許”等。
,即為模態運算元。隨著模態邏輯的非標準化即廣義模態邏輯的發展,模態運算元的定義也擴大了,諸如時態運算元“過去P”、“將來F”、“將來總是G”、拓撲運算元P、道義運算元“應該”、“必須”、“允許”等。


模態邏輯
發展歷程
模態邏輯是邏輯分支之一。研究由“必然”、“可能”等及其相關概念構成的模態命題及其推理的邏輯性質學科。模態命題與真值函項不同的是它深入命題內部反映了命題間的必然聯繫。模態邏輯是在命題邏輯和謂詞邏輯基礎上引入模態運算元及相應的公理而形成的。最基本的模態邏輯有模態命題邏輯和模態謂詞邏輯,它們相應形式化後的公理系統分別稱為模態命題演算系統和模態謂詞演算系統,是一門古老的邏輯分支。早在亞里士多德時就詳細研究過模態邏輯。他深刻分析了必然性、可能性、偶然性等模態概念,將命題分為實然命題、模態命題,而後者又分為必然命題和偶然命題,它們與A、E、I、0相結合獲得12種模態命題;仿照實然三段論建立起模態三段論,進行式、格研究。亞里士多德以後到中世紀許多學派都研究了模態邏輯,甚至還把模態概念和時間結合起來,創造出新的模態三段論系統。現代模態邏輯系統:萊布尼茨對它的建立做出了卓越貢獻,尤其是他的可能世界理論成為本世紀模態邏輯的語義理論中的基本內容。但現代模態邏輯的先驅要推19世紀末的麥柯爾,提出嚴格蘊涵等重要概念,但未提出系統。現代模態邏輯的真正創始人是美國的劉易斯。他於1914年構造了一個模態命題演算。1932年他與蘭福德合著《符號邏輯》,提出模態命題演算系統S1,S2,後來又經過修改建立S3,S4,S5等系統。他們都以“ ”(可能)作為基本符號。劉易斯之後出瑚了許多模態命題演算系統,其中T系統是一個簡單、直觀性強的系統,它是在一個完全的命題演算基礎上加上一個符號L及形成規則和兩條公理:
”(可能)作為基本符號。劉易斯之後出瑚了許多模態命題演算系統,其中T系統是一個簡單、直觀性強的系統,它是在一個完全的命題演算基礎上加上一個符號L及形成規則和兩條公理: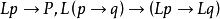 ,和一條推理規則。S4是在T之上增加公理
,和一條推理規則。S4是在T之上增加公理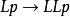 ;S5是在T之上增加公理
;S5是在T之上增加公理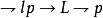 。自20世紀50年代中國的邏輯學家莫紹揆、美國的柯里等把自然推理套用到模態命題演算形成自然推理的模態命題演算。1946年,R.C.巴肯和R.卡爾納普各自獨立地構造一個模態謂詞演算系統,把模態詞和量詞結合。20世紀40年代末,卡爾納普開始從語義方面研究模態邏輯。50年代起坎格爾、欣蒂卡、克里普克等人發展了卡爾納普的理論,提出了完整的模態邏輯的語義理論。克里普克所構造的模型吸取了萊布尼茨思想,用可能世界來作為論域形成三元組(W,R,V);R指W中個體間的關係,W是可能世界集;V是滿足某些條件的賦值,用之解釋模態命題演算。又增加到D這個體域來解釋模態謂詞演算模型。60年代以來出現了許多非標準模態系統,如認知邏輯、義務邏輯、時態邏輯、道義邏輯。它們大多與哲學中認識論、倫理學等有關。
。自20世紀50年代中國的邏輯學家莫紹揆、美國的柯里等把自然推理套用到模態命題演算形成自然推理的模態命題演算。1946年,R.C.巴肯和R.卡爾納普各自獨立地構造一個模態謂詞演算系統,把模態詞和量詞結合。20世紀40年代末,卡爾納普開始從語義方面研究模態邏輯。50年代起坎格爾、欣蒂卡、克里普克等人發展了卡爾納普的理論,提出了完整的模態邏輯的語義理論。克里普克所構造的模型吸取了萊布尼茨思想,用可能世界來作為論域形成三元組(W,R,V);R指W中個體間的關係,W是可能世界集;V是滿足某些條件的賦值,用之解釋模態命題演算。又增加到D這個體域來解釋模態謂詞演算模型。60年代以來出現了許多非標準模態系統,如認知邏輯、義務邏輯、時態邏輯、道義邏輯。它們大多與哲學中認識論、倫理學等有關。

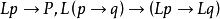
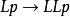
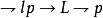
模態邏輯介紹
在客觀世界中,事物是相互聯繫、相互制約的。但有聯繫得密切與不密切的區別。人們對客觀事物的認識程度也有所不同,有些屬性是某些事物可能具有(或不具有)的;有些屬性是必然屬於(或不屬於)某一事物的。反映這種情況的形式就是模態形式,對之進行邏輯關係的分析,就是模態邏輯。
模態(modal)源出於拉丁詞modalitas,含形態、樣式和形式的意思。
模態邏輯(modal Logic)討論的可能性和必然性,不是作為命題的真值,而是作為命題和推斷的程度。
在模態邏輯中,越是在命題中添加必然性(以 表示)和可能性(以
表示)和可能性(以 表示)的成分,就越是增大了從直觀上覺察這種命題意義的正確性的困難程度,這時,開展對其形式系統的研究就變得十分重要,因而產生了現在的多種多樣的模態邏輯系統,即狹義與廣義之分。凡是涉及必然性、或然性、遺傳性和相容性的模態屬於狹義模態。在現代邏輯中,把這類模態稱為alethic模態,即真值模態。如“物體間存在著引力是必然的”、“到本世紀末我國國民生產總值翻兩番是可能的”就屬於這類模態命題。廣義模態是指命題本身所具有的非真值函項的(或非外延的)種種性質。如“子女贍養扶助父母是應該的”、“宇宙間存在著黑洞是可信的”就屬這類命題。廣義模態詞有“必 然”、“ 可能”、“必 須”、“ 應 該”“允 許”、“ 禁 止”、“ 相 信”、“ 可 疑”等。
表示)的成分,就越是增大了從直觀上覺察這種命題意義的正確性的困難程度,這時,開展對其形式系統的研究就變得十分重要,因而產生了現在的多種多樣的模態邏輯系統,即狹義與廣義之分。凡是涉及必然性、或然性、遺傳性和相容性的模態屬於狹義模態。在現代邏輯中,把這類模態稱為alethic模態,即真值模態。如“物體間存在著引力是必然的”、“到本世紀末我國國民生產總值翻兩番是可能的”就屬於這類模態命題。廣義模態是指命題本身所具有的非真值函項的(或非外延的)種種性質。如“子女贍養扶助父母是應該的”、“宇宙間存在著黑洞是可信的”就屬這類命題。廣義模態詞有“必 然”、“ 可能”、“必 須”、“ 應 該”“允 許”、“ 禁 止”、“ 相 信”、“ 可 疑”等。


如果我們在模態命題中,用小寫拉丁字母p、q、r、s....分別表示上述命題中的非模態命題,我們就獲得模態命題形式“p是必然的”、“q 是可能的”、“r 是不必然的”、“s是不可能的”。
我們可取“必然的”(以 表示)作為初始的模態詞,而“可能的”(以
表示)作為初始的模態詞,而“可能的”(以 表示)可以通過下述定義引申:
表示)可以通過下述定義引申:


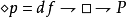
根據這個定義我們有如下公式:
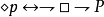
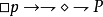
模態詞之間的邏輯關係:
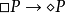
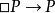
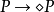
這三個公式表明了必然性、實然性、可能性的相對強度。
模態命題
模態邏輯討論的可能性與必然性,不是作為命題的真值,而是作為命題和推斷的程度。如果用符號 表示“必然性”,則有以下推理規則成立:
表示“必然性”,則有以下推理規則成立:

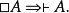
或者,如果某一公式在較狹的邏輯系統中為可以證明的,那么這一公式在更廣的邏輯系統中就可以被證明是必然成立的。從而也可以作出如下推理:
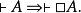
在模態邏輯中,越是在命題中添加必然性 和可能性
和可能性 的成分,就越是增大了從直觀上覺察這種命題意義的正確性的困難程度。
的成分,就越是增大了從直觀上覺察這種命題意義的正確性的困難程度。



