商格

商格(quotient lattice)亦稱因子格。由契約關係誘導出的一類格。格L的每一同態像都與L的一個商格同構。

基本介紹

• 中文名：商格
• 外文名：quotient lattice
• 領域：數學
• 學科：格論
• 別稱：因子格
• 性質：由契約關係誘導出的格

概念

商格(quotient lattice)亦稱因子格。由契約關係誘導出的一類格。設θ是格L上的一個契約關係，若L/θ={[a]θ|a∈L}表示L中由θ誘導的契約類的集合，定義：

則L/θ關於上述定義的運算∨和∧構成格，稱為L模θ的商格。格L的每一同態像都與L的一個商格同構。

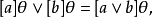
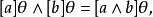
契約關係

契約關係是格的一種重要等價關係。設θ是格L的等價關係，若a≡b(θ)和a₁≡b₁(θ)，則a∧a₁≡b∧b₁(θ)和a∨a₁≡b∨b₁(θ)(替換性質)，稱θ為L的契約關係。若在格L上定義x≡y(ω)若且唯若x=y；對任意x，y有x≡y(ι)，則ω和ι是L的契約關係，稱為平凡的契約關係。若a∈L，[a]θ={x∈L|a≡x(θ)}表示包含a的契約類，則[a]θ是凸子格。對格L中的任一素理想P，均可構造出一個只含P及補集L-P兩個契約類的契約關係。此種契約關係頗為重要。它是研究格的重要工具。

格

“格”一種特殊的偏序集。在許多數學對象中，所考慮的元素之間具有某種順序。

例如，一組實數間的大小順序；一個集合的諸子集（或某些子集）間按（被包含）所成的順序 ；一組命題間按蘊涵所成的順序；等等。這種順序一般不是全序，即不是任意二元素間都能排列順序，而是在部分元素間的一種順序即偏序（半序）。偏序集和格就是研究順序的性質及作用而產生的概念和理論。

格論在代數學、射影幾何學、集合論、數理邏輯、泛函分析以及機率論等許多數學分支中都有套用。例如，在代數學中，對於一個群G與其子群格（G）之間關 系的研究。在數理邏輯中，關於不可解度的研究。

格的定義：設（L，≤）是偏序集，若L中任意兩個元素都存在上確界以及下確界，則稱（L，≤）是格（lattice），為了方便，這樣的格成為偏序格。

格論

格論論述次序及包含的性質，是布爾代數的推廣，現已成為代數的重要組成部分，並在泛函分析、賦值論、幾何、邏輯、計算機科學、圖論等方面有廣泛的套用。所謂格即指在集合L中定義兩個代數運算∨和∧，這兩個代數運算滿足：(1)a∨a = a ， a∧ a = a(冪等律);(2)a ∨ b = b ∨ a，a ∧ b=b ∧ a(交換律);(3)a ∨交換律;(3)a ∨ (b ∨ c) = (a ∨ b) ∨c，a ∧ b(b ∧ c)=(a∧b) ∧ c(結合律);(4)a ∨ (a ∧b)=a，a ∧ (a∨ b)=a(吸收律)，記作(L，≤)。格論中最重要的概念是集合上的半序關係。格的種類有分配格、模格、完全格等。

同態

設E與F為兩個群胚，它們的合成法則分別記為⊥與⊤. 稱從E到F中的映射f是群胚同態，如果對於E的任一元素偶(x，y)，有：

設E與F為兩個么半群(兩個群)，稱從E到F中的映射.f是么半群(群)的同態，如果f是群胚的同態，且E的中性元素的象是F的中性元素。(在群的情況下，後一個條件是自然滿足的，但是從加法么半群N到乘法么半群N的映射x↦0是群胚的同態， 而並不因此就是么半群的同態)。

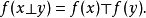
設G為乘法群，而a為G的元素. 由關係f(n)=an所定義的從加法群Z到G中的映射f是群的同態。

設A與B為兩個環(兩個體)，稱從A到B中的映射f是環(體)的同態，如果f是加法群的同態，且為乘法么半群的同態. 這就是說，對A的任一元素偶(x，y)，有：

並且f將A的單位元變成B的單位元。

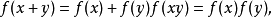
例如，設n為非零自然數；使任一有理整數對應其對模n的剩餘類映射是從環Z到環Z/nZ上的同態。設E與F為兩個A-代數(兩個酉A-代數)。稱從E到F中的映射f是A-代數(酉A-代數)的同態，如果它是線性映射，並且是乘法群胚(乘法么半群)的同態。

例如，設E為交換體K上的非零有限n維向量空間，而B為E的基. 則從E的全體自同態之酉代數ℒ(E)到K中元素構成的全體n階方陣之酉代數Mn (K)中的映射，如果該映射使E的任一自同態對應它在基B中的矩陣，則這一映射是酉代數的同態。同態的概念能用抽象的方式加以推廣。