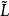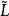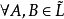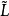子格(sublattice)一種組合構形，設(L，∧，∨)是格，S是L的非空子集，若S關於L 中的運算∧，∨仍構成格，則稱S是L的子格。其中∧，∨分別是求最大下界和最小上界運算。
凸子格(convex sublattice)具有特殊性質的一類子格。
基本介紹
- 中文名：凸子格
- 外文名：convex sublattice
- 領域：代數學中的格論
- 定義：具有特殊性質的子格
- 相關概念：冪格
- 實例：區間、半開區間、開區間
格與格論,子格的概念,凸子格的定義,冪格與凸子格,
格與格論
格是有著廣泛套用的一類偏序集。它是具有兩個二元運算的代數系。設L是偏序集，若L的任兩個元素均有上確界及下確界，則稱L為格，記為(L;≤)，簡記為L.a，b∈L，{a，b}的上、下確界分別記為a∨b(即sup{a，b})及a∧b(即inf{a，b})。格亦可用恆等式來定義，它是由戴德金(Dedekind，J.W.R.)給出的。若代數系L有兩個代數運算∧，∨，且對任意a，b，c∈L，滿足下列恆等式：
L1 | a∧a=a，a∨a=a; | (冪等律) |
L2 | a∧b=b∧a，a∨b=b∨a; | (交換律) |
L3 | a∧(b∧c)=(a∧b)∧c， | |
a∨(b∨c)=(a∨b)∨c; | (結合律) | |
L4 | a∧(a∨b)=a，a∨(a∧b)=a; | (吸收律) |
則稱L為格，記為(L;∧，∨)，簡記為格L。上述兩種定義是等價的。1951年，索金(Sorkin，Ju.I.)用僅含三個變數的四個恆等式刻畫了格；1972年，沛德邁耐罕(Padmanabhan，R.)發現可用僅含三個變數的兩個恆等式刻畫格，但不能用少於三個變數的兩個恆等式刻畫格。19世紀末，皮爾斯(Peirce，C.S.)和施洛德(Schro¨der，F.W.K.E.)在研究布爾代數的公理化以及戴德金研究代數數的理想時獨立地提出了格的概念；1897年，戴德金首先對格進行了研究。在20世紀30年代中期，伯克霍夫(Birkhoff，G.D.)的著作開始了格論的全面發展，他的一系列文章展示了格論的重要性，並使格論成為代數學的一門重要分支。
子格的概念
子格是格論的基本概念之一。設S是格L的子集，若S關於L中的二元運算∧和∨是封閉的，即對任意a，b∈S，a∧b，a∨b∈S，則稱S為L的子格；若子格S含0，1，則稱S為格L的{0，1}-子格。若a，b∈L，a≤b，則[a，b]={x∈L|a≤x≤b}是L的子格，稱為閉區間。同樣可定義半開區間(a，b]和[a，b)以及開區間(a，b)。設H為格L的非空子集，L中一切包含H的子格的交，稱為L的由H生成的子格，記為[H]；稱H為[H]的一個生成系。設S是格L的子格，若除L外，沒有真包含S的子格，則稱S為L的極大子格。格L的一切極大子格的交集Φ(L)稱為弗拉梯尼子格。格L的所有子格按集合的包含關係構成格，記為Sub(L)。
凸子格的定義
設S是偏序集P的子集，a,b∈s，若a≤b，有[a，b]
S，則稱S為P的凸子集。設S是格L的子集，若a，b∈S時有[a∧b，a∨b]
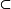S，則稱S為L的凸子格。設H是格L的非空子集，L中包含H的所有凸子格的交集仍是凸子格，稱為由H生成的L的凸子格。區間、半開區間、開區間都是凸子格。
冪格與凸子格
冪格與凸子格之間主要存在以下定義和定理：
定義1 設(L;∨,∧)是一個格，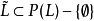
，在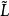
中定義運算：
，
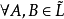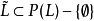
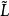
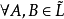
A∨B={a∨b|a∈A,b∈B}；A∧B={a∧b|a∈A,b∈B}
若（
；∨,∧）是一個格，則稱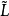
為L上的一個冪格。
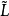
定義2 設(L;∨,∧)是一個格，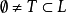
，S是L的一個子格，若
，
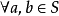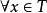，由a∧b≤x≤a∨b，可以推出x∈S，則稱S為L的相對於T的凸子格。
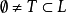
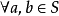
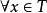
若S是L的凸子格，則S必是L的相對於T的凸子格。
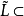
定理2 設(L;∨,∧)是一個分配格，T是L的一個子格，令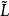
={A|A是T的非空凸子格}，則(
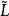;∨,∧)是L上的一個冪格。
