哥德爾本體論證明

哥德爾本體論證明是數學家庫爾特·哥德爾對11世紀義大利僧侶聖安瑟倫對於神存在性的本體論論點整理並改進後所作的數學表達方式。聖安瑟倫後曾有17世紀的萊布尼茨提出了另一個較複雜的宇宙論證版本，而這個就是哥德爾所研究並嘗試用其本體論邏輯論點去澄清的版本。

雖然哥德爾有宗教信仰，他從未發表這個證明。他在1970年代絕食而死的前幾年不斷將這個論點向身邊的朋友們展示，他去世九年後，即1987年，這論點才被出版。

基本介紹

• 中文名：哥德爾本體論證明
• 外文名：Gödel's ontological proof
• 提出者：庫爾特·哥德爾
• 提出時間：11世紀

簡介

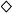哥德爾的論證證明用上了由他本人及克里普克等20世紀邏輯學家所發展的模態邏輯，分開了必需的真與偶然的真。表示必然性，而表示可能性。證明的關鍵在於利用“神可能存在”（定理2）及神的極致性（定義1）去推導出“神必然存在”（定理4）。在S5模態邏輯系統的框架下，這項結論可謂全然有效，因此相當驚人。然而，若使用相同的邏輯推論去假設極致偉大的存有不存在，也同樣沒有任何自相矛盾之處。

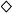
證明

聖安瑟倫的論點

11世紀的義大利僧侶聖安瑟倫，其論點用最簡潔的表達如下：“God, by definition, is that than which a greater cannot be thought（i.e.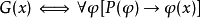）. God exists in the understanding（i.e.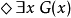）. If God exists in the understanding, we could imagine Him to be greater by existing inreality. Therefore, God must exist.”。也就是：

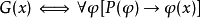
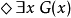
1：神是我們所能想像得到最偉大的存有。

2：實際存在的物體比想像中的物體更偉大。

推論：神存在。

哥德爾的證明

哥德爾的證明若以符號表達，則如下：

解「像神特性」，及為任一特性，解 「為正（也可作「善」或「偉大」）特性」， 解「 x 擁有特性」，解「必需存在」，解 「是 x 的本質（essence）」，表示「必然性」，而 表示「可能性」:

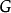
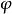
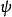
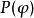
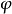
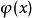
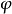
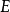
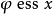
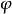
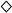
證明中用到的公設

哥德爾證明中的公設有5項：

• 公設 0: 在所有特性中挑出正特性是可能的。哥德爾定義正特性頗不清晰：“正解作在道德美學上為正（independently of the accidental structure of the world）......It may also mean pureattributionas opposed toprivation(or containing privation)." (Gödel 1995)
  

然後我們假設對於所有正特性，以下幾個條件正確（可被總結為“那些正特性們形成了一個超濾子”）：

• 公設 1: 假如φ為正特性且φ導出ψ，那ψ也是正。
  
• 公設 2: 假如φ是一個特性，那要么φ與其邏輯非——“非φ”，有一個且只有一個為正特性。
  
• 公設 3: “像神特性”G乃是正特性
  
• 公設 4: 若φ為正特性，則其必需為正特性。
  
• 公設 5: 必需存在性E是一個正特性。This mirrors the key assumption in Anselm's argument.
  

批評

對哥德爾本體論證明的大部分批評，皆在於其公設部分。正如任何邏輯系統，假如其所依賴的公設備受懷疑，則結論也會受到懷疑。此情況特別適用於哥德爾的證明，因為其所依賴的5條公設，全部也是可以質疑的。此證明並不表示其結論正確，但假如你接受了那些公設，結論就是正確的。