有兩種非常不同類型的超濾子: 主要的和自由的。主要(或固定或平凡)的超濾子是包含最小元的濾子。因此主超濾子有形式Fa={x|a≤x}對於給定偏序集合的某些(但非全部)元素。
基本介紹
- 中文名：超濾子
- 外文名：ultrafilter
- 適用範圍：數理科學
定義,基本信息,類型和存在性,套用,
定義
無窮集合 X 上的超濾子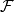
是 X 的子集的類，且滿足以下條件：
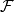
①
；
②如果
和
，那么
；
③如果 A，，那么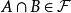
；
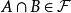
④任給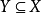
，或者
或者 X\
。
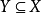
超濾子中最常用的是自由超濾子。如果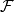是 X 上的超濾子且對每一個
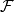集合 {x}不在中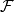，就被稱為 X 上的自由超濾子。在策梅洛-弗倫克爾公理系統的基礎上，無限集 X 上自由超濾子的存在性是選擇公理的推論。
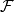
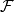
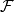
基本信息
在數學領域集合論中，在集合 X 上的超濾子是作為極大濾子的 X 子集的蒐集。超濾子可以被認為是有限可加性測度。那么 X 的所有子集要么被認為是“幾乎所有”(有測度 1)要么被認為是“幾乎沒有”(有測度 0)。如果 A 是 X 的子集，則要么 A 要么 X\A 是超濾子的元素(這裡 X\A 是 A 在 X 中的相對補集；就是說，X 的不在 A 中的所有元素的集合)。這個概念可以被推廣到布爾代數甚至是一般偏序，並在集合論、模型論和拓撲學中有很多套用
類型和存在性
有兩種非常不同類型的超濾子: 主要的和自由的。主要(或固定或平凡)的超濾子是包含最小元的濾子。因此主超濾子有形式 Fa={x | a≤x} 對於給定偏序集合的某些(但非全部)元素 a。在這種情況下 a 被稱為超濾子的“主元素”。對於濾子在集合上的情況，有資格成為主元素的精確的是一元素集合。因此在集合 S 上的主超濾子由包含 S 的特定點的所有集合構成。在有限集合上的超濾子是主要的。不是主要的任何超濾子叫做自由(或非主要)超濾子。
可以證明所有濾子(或更一般的說，帶有有限交集性質的任何子集)都包含在一個超濾子中(參見超濾子引理)並且自由超濾子因而存在，但是這個證明涉及佐恩引理形式的選擇公理。因此不能給出自由主濾子的明確例子。經管如此，在無限集合上的幾乎所有超濾子都是自由的。相反的，在有限偏序集合(或在有限集合上)的所有超濾子都是主要的，因為任何有限濾子都最小元素。
套用
在集合上的超濾子套用於拓撲學特別是聯繫於緊緻豪斯多夫空間，和模型論中超乘積的構造。在緊緻豪斯多夫空間上的所有超濾子會聚到精確的一個點。類似的，在偏序集合上超濾子是非常重要的，如果這個偏序集合是布爾代數，因為這種情況下超濾子同一於素濾子。這種形式的超濾子在Stone布爾代數表示定理中扮演中心角色。
在偏序集合 P 上所有超濾子 G 可以按自然方式來拓撲化，這實際上密切關聯於上述表示定理。對於 P 的任何元素 a，設 Da = { U ∈ G | a ∈ U }。這是在 P 還是布爾代數時最有用的，因為在這種情況下所有 Da 的集合是在 G 上的緊緻豪斯多夫拓撲的基。特別是，在考慮在集合 S 上的超濾子的時候(就是說 P 是 S 的冪集並按集合包含排序)，結果的拓撲空間是勢為 |S| 的離散空間的 Stone-Čech緊緻化。
在模型論中的超乘積構造使用超濾子來生成結構的基本擴張。例如，在構造超實數為實數的超乘積中，我們首先把論域從實數擴展到實數序列。這個序列空間被當作實數的超集，通過用對應的常量序列來識別每個實數。要把熟悉的函式和關係(比如 + 和 <)從實數擴展到超實數，自然的想法是逐點的定義它們。但是這會丟失實數的重要邏輯性質；比如逐點 < 不是全序。所以我們轉而“逐點模 U”的定義函式和關係，這裡的 U 是在序列的索引集上的超濾子；通過Łoś定理，這保持了實數可以用一階邏輯陳述的所有性質。如果 U 是非主要的，則從而獲得的擴展是非平凡的。
