哈希樹

在計算機科學中，哈希樹（或哈希特里）是一種持久性數據結構，可用於實現集合和映射，旨在替換純函式式編程中的哈希表。 在其基本形式中，哈希樹在trie中存儲其鍵的哈希值（被視為位串），其中實際鍵和（可選）值存儲在trie的“最終”節點中

基本介紹

• 中文名：哈希樹
• 外文名：Hash tree

介紹

在將一個數進行哈希的時候，我曾經寫過關於哈希的這么些東西：對於數，當一個質數不夠用的時候，可以加上第二個質數，用兩個mod來確定該數據在庫中的位置。那么這裡需要簡單的解釋一下，對於一個質數x，它的mod有[ 0 .. x - 1 ] x種；所以對於兩個質數x和y，能存儲的無一重複的數據有 x*y 個，其實也就是開一個x*y的二維數組。但是當數據極其多時，用兩個質數去mod顯然也是有不夠的時候，就還要再加一個。為了便於查找，選取最小的十個質數，也就是2，3，5，7，11，13，17，23，29，31來mod，能包括的數就有10555815270個，已經遠超出longint了。就是說，如果我開一個十維數組，那么取到一個數的效率就是O( 1 )！但是那樣顯然太浪費空間了，就可以用到樹。

圖1

同一節點中的子節點，從左到右代表不同的餘數結果。例如：第二層節點下有三個子節點。那么從左到右分別代表：除3餘0，除3餘1和除3餘2。

對質數的餘數決定了處理的路徑。例如：某個數來到第二層子節點，那么它要做取余操作，然後再決定從哪個子節點向下搜尋。如果這個數是12那么它需要從第一個子節點向下搜尋；如果這個數是7那么它需要從第二個子節點向下搜尋；如果這個數是32那么它需要從第三個子節點向下搜尋。這就是一個哈希樹了。

哈希樹的建立

選擇質數分辨算法來建立一棵哈希樹。選擇從2開始的連續質數來建立一個十層的哈希樹。第一層結點為根結點，根結點下有2個結點；第二層的每個結點下有3個結點；依此類推，即每層結點的子節點數目為連續的質數。到第十層，每個結點下有29個結點。同一結點中的子結點，從左到右代表不同的餘數結果。例如：第二層結點下有三個子節點。那么從左到右分別代表：除3餘0，除3餘1，除3餘2.對質數進行取余操作得到的餘數決定了處理的路徑。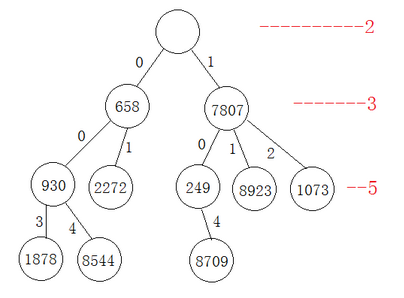

圖2

以隨機的10個數的插入為例，來圖解HashTree的插入過程。如圖2。

其實也可以把所有的鍵-值節點放在哈希樹的第10層葉節點處，這第10層的滿節點數就包含了所有的整數個數，但是如果這樣處理的話，所有的非葉子節點作為鍵-值節點的索引，這樣使樹結構龐大，浪費空間。

查找

哈希樹的節點查找過程和節點插入過程類似，就是對關鍵字用質數序列取余，根據餘數確定下一節點的分叉路徑，直到找到目標節點。
如上圖，最小”哈希樹(HashTree)在從4G個對象中找出所匹配的對象，比較次數不超過10次。也就是說：最多屬於O(10)。在實際套用中，調整了質數的範圍，使得比較次數一般不超過5次。也就是說：最多屬於O(5)。因此可以根據自身需要在時間和空間上尋求一個平衡點。

刪除

哈希樹的節點刪除過程也很簡單，哈希樹在刪除的時候，並不做任何結構調整。
只是先查到到要刪除的節點，然後把此節點的“占位標記”置為false即可（即表示此節點為空節點，但並不進行物理刪除）。

優點

1、結構簡單

從哈希樹的結構來說，非常的簡單。每層節點的子節點個數為連續的質數。子節點可以隨時創建。因此哈希樹的結構是動態的，也不像某些哈希算法那樣需要長時間的初始化過程。哈希樹也沒有必要為不存在的關鍵字提前分配空間。

需要注意的是哈希樹是一個單向增加的結構，即隨著所需要存儲的數據量增加而增大。即使數據量減少到原來的數量，但是哈希樹的總節點數不會減少。這樣做的目的是為了避免結構的調整帶來的額外消耗。

2、查找迅速

從算法過程我們可以看出，對於整數，哈希樹層級最多能增加到10。因此最多只需要十次取余和比較操作，就可以知道這個對象是否存在。這個在算法邏輯上決定了哈希樹的優越性。
一般的樹狀結構，往往隨著層次和層次中節點數的增加而導致更多的比較操作。操作次數可以說無法準確確定上限。而哈希樹的查找次數和元素個數沒有關係。如果元素的連續關鍵字總個數在計算機的整數（32bit）所能表達的最大範圍內，那么比較次數就最多不會超過10次，通常低於這個數值。

3、結構不變

從刪除算法中可以看出，哈希樹在刪除的時候，並不做任何結構調整。這個也是它的一個非常好的優點。常規樹結構在增加元素和刪除元素的時候都要做一定的結構調整，否則他們將可能退化為鍊表結構，而導致查找效率的降低。哈希樹採取的是一種“見縫插針”的算法，從來不用擔心退化的問題，也不必為最佳化結構而採取額外的操作，因此大大節約了操作時間。

缺點

哈希樹不支持排序，沒有順序特性。如果在此基礎上不做任何改進的話並試圖通過遍歷來實現排序，那么操作效率將遠遠低於其他類型的數據結構。