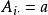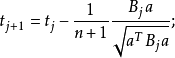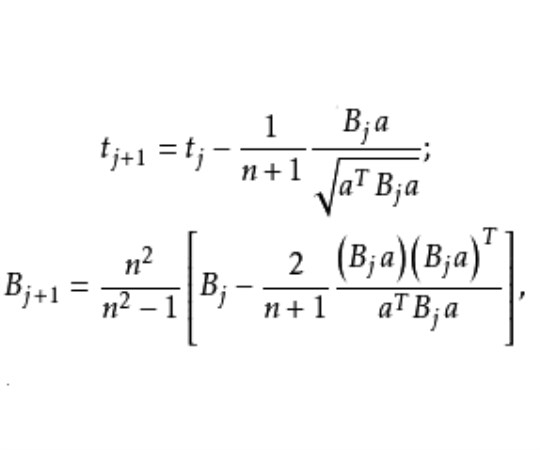哈奇揚方法(Khachyian method)亦稱橢球法，它是蘇聯學者肖爾關於非線性規劃的橢球方法的基礎上提出的，指一種疊代路徑迥然異於單純形方法的求解線性規劃的多項式算法。
基本介紹
- 中文名：哈奇揚方法
- 外文名：Khachyian method
- 所屬學科：數學
- 所屬問題：線性規劃
- 別稱：橢球法
基本特點,方法步驟,
基本特點
它具有如下的特點：
1.它是通過包含線性規劃約束條件構成的多面體的橢球搜尋最優解，不同於單純形方法是從該多面體的一個頂點疊代到相鄰的一個頂點。
2.疊代過程始終保持一個橢球，每疊代一次都得到一個具有相同性質的更小的橢球，因此，人們常把這個方法稱為求解線性規劃的橢球方法。
3.從算法複雜性的觀點看，它是多項式算法，而單純形方法並不是多項式算法。
此方法由蘇聯學者哈奇揚(Л.Г.Хачиян)於1979年給出，所以得此名。
方法步驟
哈奇揚方法為考慮如下特徵的問題：求x使之滿足
，其中A為
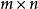矩陣，其方法步驟為：
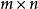
1.(初始準備)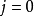 
記錄疊代次數，tj為第j次疊代的解，初始解
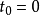為分量全為0的n維列向量，取
為n階對角矩陣，其中I為n階單位陣，
為問題的規模，P為矩陣A及向量b中所有非零分量的乘積，在上述數據中，可逆方陣B是構造橢球的關鍵成分，初始橢球
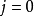
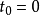
2.(檢驗) 若tj滿足
，則停止疊代，當前解即為所求，若
，則停止疊代，說明問題無解。
3.(疊代) 任選一個不滿足的不等式，例如
，並記
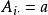，設
