周角不等式

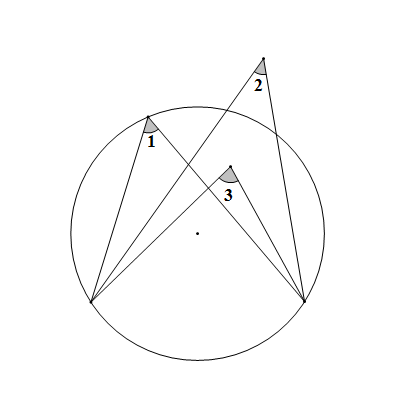
周角不等式 圓內弧所對的圓周角不等於平面內不在該圓上的任一點與該弧兩端連線的夾角，且當點在圓外時，夾角小於圓周角；點在圓內時，夾角大於圓周角。

基本介紹

• 中文名：周角不等式
• 適用領域：數學-幾何
• 套用學科：數學

內容

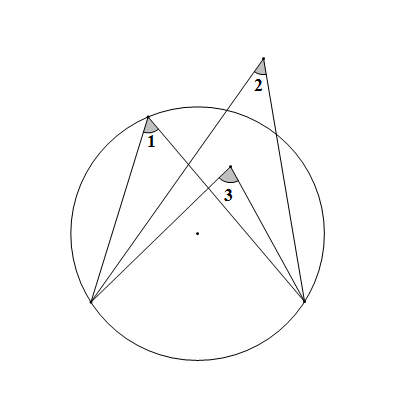
圖1

即如圖1，∠2＜∠1＜∠3

推導過程

證明：

為使證明簡便，將圓上、圓外和圓內三點平移至同一直線上。

圖2

如圖2，點P、Q、R分別在圓上、圓外和圓內，且在同一直線上。

由三角形外角定理，得：

∠3=∠1+∠PBR＞∠1；

∠2=∠1-∠PBQ＜∠1。

綜上，∠2＜∠1＜∠3，

原命題得證。

套用

可作為判斷點與圓的位置關係的依據，拓展開來則可以在證明點共圓等問題時起到作用。