基本介紹
- 中文名:周期攝動
- 外文名:periodic perturbation
- 學科:工程技術
- 定義:攝動項中時間的周期函式項
- 攝動:受到外界影響在軌道上產生的偏差
- 分類:短周期攝動、長周期攝動
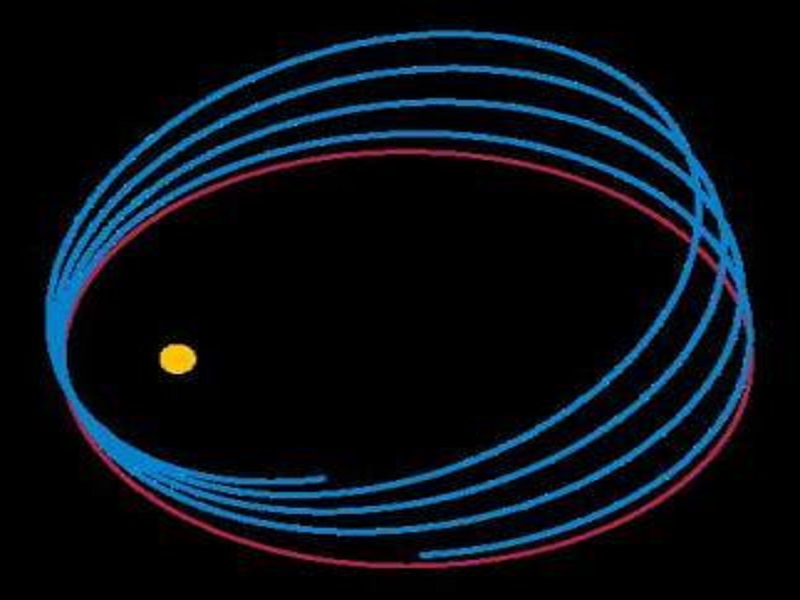
天體在攝動作用下,其坐標、速度或軌道要素都產生變化,這種變化成分稱為攝動項。周期攝動就是指天體坐標,速度或軌道要素的攝動量中隨時間作周期變化的部分。周期攝...
周期攝動中周期長於軌道周期的部分。...... 周期攝動中周期長於軌道周期的部分。中文名稱:長周期攝動;英文名稱:longperiodperturbation;V百科往期回顧 詞條統計 瀏...
位規則的橢球體,作用於衛星的地球引力不通過地心,還有月球及太陽引力、地球大氣阻力、太陽光壓等作用於衛星,使其運動軌道偏離克卜勒軌道形成或長或短的周期性攝動。...
現代天體力學的一個分支。人造地球衛星是一種圍繞地球作圓或橢圓運動的人造小天體。如果地球是一個密度均勻的正球體,又沒有其他因素的攝動,則人造衛星的運動就是...
地球引力位的球諧函式展開式中次為零的位係數。帶諧函式描述攝動函式隨緯度的變化,它沿緯度有正負交替。...
由於攝動力的影響,衛星的運動軌道比較複雜。按攝動理論,軌道要素不再是常數。根據軌道要素的變化特點,軌道攝動可以分為長期攝動、長周期攝動、短周期攝動(見航天...
因此,為了尋求最優的軌跡保持策略,延長軌跡保持周期,對LEO衛星所受攝動力進行了詳細的分析,在傾角偏置改善降交點地方時的同時,對其影響星下點軌跡漂移以及半長軸衰減...
GPS衛星的運動在二體運動的基礎上加入了長期攝動和周期攝動,其中主要的周期攝動是周期約六小時的二階帶諧項引起的短周期攝動。[1] ...
在木星和土星的相互攝動中就出現這種情況,它們的平均角速度比值接近5:2,因而產生顯著的長周期攝動,對木星為1,196″,對土星達到2,908″,周期約為890年。計算...
地球引力位的帶諧部分主要引起衛星軌道的長期和周期攝動,田諧部分只產生幅度較小的短周期攝動。從衛星運動理論知道,地球引力位的偶次帶諧係數引起衛星軌道升交點...
