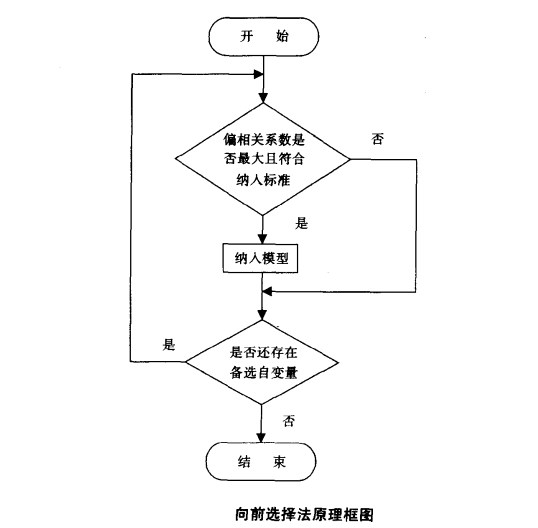
向前選擇法是一種回歸模型的自變數選擇方法，其特點是把候選的自變數逐個引入回歸方程，故稱向前法。具體操作步驟是：先把與因變數y有最大相關係數的自變數擬合模型，進行回歸係數的顯著性檢驗，決定是否把該自變數引入模型；然後，在未被引進模型的自變數中，對與y有最大偏相關係數的自變數引入模型並進行回歸係數的顯著性檢驗，決定取捨，依次類推。直至在排除了已選入變數對y的影響之後，未選入自變數對y的回歸係數的顯著性檢驗結果都不顯著異於0為止。這種方法比較簡單，但主要缺點是，如果存在多重共線性，最後的模型中可能混有不太重要的自變數。
基本介紹
- 中文名：向前選擇法
- 外文名：forward selection
- 簡介：一種回歸模型的自變數選擇方法
- 所屬學科：數學
- 所屬問題：數理統計
- 特點：把候選的自變數逐個引入回歸方程
- 相關概念：向後選擇法，逐步回歸法等
基本介紹,基本步驟,
基本介紹
在實際問題中，選擇合適的變數來建立回歸方程，不是一件很容易的事情。因為影響因變數y的因素很多，而這些因素之間存在著多重共線性，特別是在教育和經濟類數據中，各自變數之間有高度的相互依賴性，這樣會給回歸係數估計值帶來不合理的解釋。為了得到一個穩健的、可靠的回歸模型，這就需要給出一種方法，使得能從眾多的影響y的因素中挑選出對y影響大的變數，在它們和y的觀測數據基礎上建立最優的回歸方程。向前選擇法與向後剔除法、逐步回歸法一樣是目前使用較為廣泛的在眾多因素中篩選對因變數有顯著影響的自變數的統計方法。在向前選擇法中，與因變數有最大正相關或最大負相關的變數首先進入回歸方程，然後按假設H0：“進入回歸方程的變數的係數為0”對進入回歸方程的變數的係數進行F-檢驗。為了決定變數(及每一個後繼變數)是否能進入回歸方程，須指定進入回歸方程的判別標準。常用的標準有：①F值進入標準FIN：當F統計量值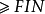
(臨界值，常指定為3.84)時，變數才可能進入回歸方程；②F機率進入標準PIN：當F統計量的相伴機率≤PIN(臨界機率，常指定為0.05)時，變數才可能進入回歸方程。如果第一個被選變數滿足F檢驗條件(即H0被拒絕)，則向前選擇變數過程繼續；否則，選擇變數過程結束，回歸方程中無任何自變數。一旦有一個自變數進入回歸方程，接著考察因變數與不在方程中的每個變數的偏相關係數，具有最大偏相關係數的變數是下一個候選者。如果滿足F檢驗條件，則該變數進入回歸方程，且重複上述選擇過程。當沒有變數滿足F檢驗條件時，選擇變數過程終止。此時所得到的回歸方程為最優回歸方程。
基本步驟
向前選擇法是以不存在自變數的模型作為起點，然後逐步增加自變數並篩選自變數的過程。具體過程如下：
1．對k個自變數
分別擬合對因變數y的一元線性回歸模型，即得到k個一元線性回歸模型，然後找出F統計量值最高的模型及對應的
，並將該自變數首先引入模型中。在此過程中，需要注意的是：如果所有模型的F統計量均未通過檢驗，說明所蒐集的自變數與因變數之間均為不顯著，說明模型構建不適合，應當考慮換其他模型，本方法的運算過程也就終止了。
2．在已經引入的模型上，分別引入剩餘的k-1個自變數，分別得到k-1個二元線性回歸模型，即變數組合為k-1個二元線性回歸模型，繼而得到k-1個新的F統計量，並從中找出F統計量的值為最高的模型，此時，該模型中含有兩個自變數，新增加的自變數即為經過篩選出來的應當引入模型的自變數。同樣地，如果在此過程中，沒有F統計量通過檢驗，則運算終止。
3．按照第二步的篩選方法，不斷引入新的自變數，直到引入的新的自變數也不能使得殘差平方和(SSE)顯著減少為止（F統計量均為通過檢驗）。向前選擇法就是這樣一個不斷引入新變數，進行F統計量檢驗的過程，由此可見，只要某個自變數增加到模型中，該自變數就一定會保留在模型中。
