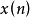同態處理

一種特定的數位訊號處理方法.利用同態系統把一類輸入信號變換為另一類信號輸出的過程稱為同態信號處理。例如，對輸入為乘法組合的信號或者卷積組合的信號，通過同態系統就可以得到另一種組合的輸出信號。同態系統可以把非線性組合的信號，通過變換用線性系統對它進行處理。

基本介紹

• 中文名：同態處理
• 外文名：homomorphic signal processing
• 學科：信息與通信
• 套用領域：通信、圖像處理

簡介

用同態系統進行信號處理。同態系統是服從廣義疊加原理、在代數運算上可用輸入和輸出的矢量空間之間的線性變換來表征的非線性系統。對於卷積性信號，其頻譜是相互疊加在一起的。不能通過簡單的濾波器將其分開，需要對信號進行同態處理。

同態處理又稱同態信號處理。在信號處理中，常需從帶有噪聲的信號中提取原始信號。一般用濾波處理方法濾除或削弱噪聲干擾以及其他不需要的信號。對於疊加性組合信號，可用線性濾波器將它們分離開。對於實用中常見的非疊加性 組合信號（如乘積性信號和褶積性信號），靠線性濾波器分離或處理這些信號分量往往是無效的，這時應採用非線性濾波，即要用同態濾波處理系統進行信號處理。在輸入輸出運算相同的情況下，同態系統可分為相乘信號的同態濾波處理和褶積信號的同態濾波處理兩種。

在許多實際問題中，信號為兩個或多個分量的乘積（如在有衰落的傳輸信道中，衰落效應可看作一個緩變分量和傳輸信號相乘）。對這類相乘信號，如用線性系統來分離信號各成分或單獨地改善某一信號成分往往是無效的。但利用相乘信號的同態濾波處理，就可以取得較好的濾波效果。在多徑或混響環境中進行通信、定位或記錄，產生失真的效果可以看成是干擾與所需信號的褶積，對這類信號可用褶積信號的同態濾波處理。在語音、圖像、雷達、聲吶、地震勘探以及生物醫學工程等領域中，同態信號處理獲得廣泛的套用。

算法步驟

比如語音信號可以視為聲門激勵信號與聲道衝激回響的卷積。同態語音信號分析的目的就是將激勵源與聲道衝激回響分開來分別進行研究，儘量獲得準確的激勵源與聲道衝激回響的估計，這也成為解卷算法。

解卷算法分為兩大類：

一類是為線性系統建立模型，然後按照某種準則對模型進行參數估計，即“參數解卷”，比如線性預測分析技術。

二類是無須建立模型。稱之為”非參數解卷“。同態處理就是其中的一種。它可以實現將激勵源與聲道衝激回響的卷積關係變換為求和關係，通過濾波進一步分離兩種信號。

假設輸入信號為：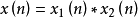

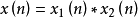
它採用三步數學運算：

1、Z變換：時域中的將卷積運算轉換為頻域中的乘積運算。

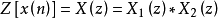
2、對數運算：將乘積運算轉換為加性運算。

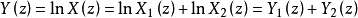
3、逆Z變換：將頻域轉換到時域中來。

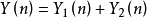
其中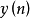是一個時間序列的Z變換的對數所對應的時間序列，稱為復倒譜。

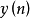
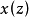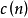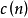如果忽略的相位信息，只考慮幅度信息，那么立刻得到倒譜的定義：定義為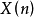 Z變換後的幅度的對數的逆Z變換，即

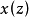
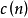
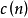
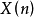
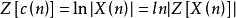
同態系統原理

利用同態系統進行圖像增強處理是把頻率過濾和灰度變換結合起來的一種處理方法。它是把圖像的照明反射模型作為頻域處理的基礎，利用壓縮亮度範圍和增強對比度來改善圖像的一種處理技術。

由於子系統是“確定的一種特徵系統，因此稱為對運算的特徵系統。同樣是對運算的特徵系統。顯然，具有相同運算規則的第一子系統和第三子系統的所有同態系統，只是其線性系統部分有所不同。換言之，特徵系統確定之後，剩下的就是線性濾波問題了。

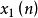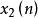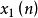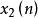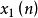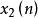因此，為了分離 和 ，必須用一個線性濾波器L來完全分離 和 。理想的分離取決於運算法則“囗”以及輸入信號分量 和 的性質。

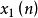
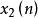
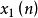
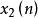
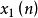
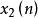
同態濾波處理系統 在輸入和輸出運算相同的情況下，同態系統可分為相乘信號的同態濾波處理和褶積信號的同態濾波處理兩種。

套用

在許多實際問題中，信號為兩個或多個分量的乘積。例如，在有衰落的傳輸信道中，衰落效應可以看作是一個緩變分量和傳輸信號相乘。又如，調幅信號可表示為載頻信號與包絡函式的乘積，在接收機內需要分離載波和包絡。在這一類相乘信號中，用線性系統來分離信號各成分或單獨地改善某一信號成分往往是無效的。但利用相乘信號的同態濾波處理，就可以取得較好的濾波效果。

褶積信號的同態濾波處理 　在多徑或混響環境中進行通信、定位或記錄，產生失真的效果可以看成是干擾與所需信號的褶積。在語音信號處理中，經常要分離激勵源與聲道衝激回響，至少在一段短時間內可以認為語音波形是由兩者的褶積構成的。地震記錄數據是地震子波與含有岩層結構信息的反射係數序列的褶積組合。離散褶積組合信號可以表示為 。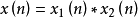

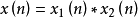
Z變換運算也可以看作是一個系統，它的輸入運算為褶積，輸出運算是乘法的同態變換。因此，利用Z變換就能把褶積組合變換成乘法組合，從而可以利用上述乘法同態濾波系統來處理。但是，通常函式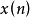 是個複數，故不得不採用複對數運算。