基本介紹
- 中文名:同態加密
- 外文名:Homomorphic Encryption
- 術語分類:密碼學
- 主要套用:雲計算、電子商務、物聯網等
概念,相關概念,主要套用,
概念
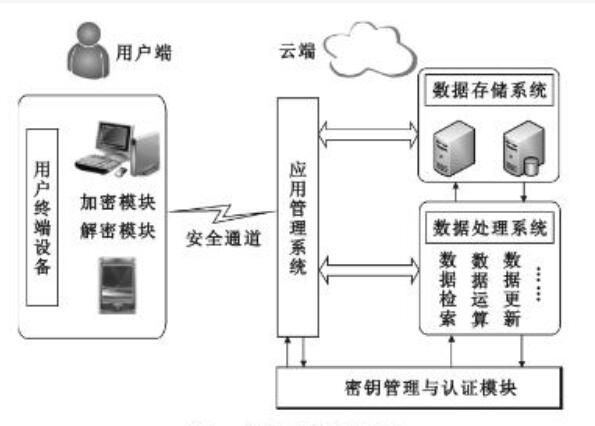
隨著網際網路的發展和雲計算概念的誕生,以及人們在密文搜尋、電子投票、移動代碼和多方計算等方面的需求日益增加,同態加密(Homomorphic Encryption)變得更加重要。同態加密是一類具有特殊自然屬性的加密方法,此概念是Rivest等人在20世紀70年代首先提出的,與一般加密算法相比,同態加密除了能實現基本的加密操作之外,還能實現密文間的多種計算功能,即先計算後解密可等價於先解密後計算。這個特性對於保護信息的安全具有重要意義,利用同態加密技術可以先對多個密文進行計算之後再解密,不必對每一個密文解密而花費高昂的計算代價;利用同態加密技術可以實現無密鑰方對密文的計算,密文計算無須經過密鑰方,既可以減少通信代價,又可以轉移計算任務,由此可平衡各方的計算代價;利用同態加密技術可以實現讓解密方只能獲知最後的結果,而無法獲得每一個密文的訊息,可以提高信息的安全性。正是由於同態加密技術在計算複雜性、通信複雜性與安全性上的優勢,越來越多的研究力量投入到其理論和套用的探索中。近年來,雲計算受到廣泛關注,而它在實現中遇到的問題之一即是如何保證數據的私密性,同態加密可以在一定程度上解決這個技術難題。
本質上,同態加密是指這樣一種加密函式,對明文進行環上的加法和乘法運算再加密,與加密後對密文進行相應的運算,結果是等價的。由於這個良好的性質,人們可以委託第三方對數據進行處理而不泄露信息。具有同態性質的加密函式是指兩個明文a、b滿足Dec(En(a)⊙En(b))=a⊕b的加密函式,其中En是加密運算,Dec是解密運算,⊙、⊕分別對應明文和密文域上的運算。當⊕代表加法時,稱該加密為加同態加密:當⊙代表乘法時,稱該加密為乘同態加密。
全同態加密是指同時滿足加同態和乘同態性質,可以進行任意多次加和乘運算的加密函式。用數學公式來表達,即Dec(f(En(m1),En(m2),…,En(mk)))=f(m1,m2,…,mk),或寫成:f(En(m1),En(m2),…,En(mk))=En(f(m1,m2,…,mk)),如果f是任意函式,稱為全同態加密。
直到2009年,IBM的研究人員Gentry首次設計出一個真正的全同態加密體制,即可以在不解密的條件下對加密數據進行任何可以在明文上進行的運算,使得對加密信息仍能進行深入和無限的分析,而不會影響其保密性。經過這一突破,存儲他人機密電子數據的服務提供商就能受用戶委託來充分分析數據,不用頻繁地與用戶互動,也不必看到任何隱私數據。同態加密技術允許公司將敏感的信息儲存在遠程伺服器里,既避免從當地的主機端發生泄密,又依然保證了信息的使用和搜尋;用戶也得以使用搜尋引擎進行查詢並獲取結果,而不用擔心搜尋引擎會留下自己的查詢記錄。為提高全同態加密的效率,密碼學界對其研究與探索仍在不斷推進,這將使得全同態加密越來越向實用化靠近。
相關概念
同態加密的思想起源於私密同態,代數同態和算術同態是私密同態的子集。
R 和 S 是域,稱加密函式 E:R→S 為:
加法同態,如果存在有效算法⊕,E(x+y)=E(x)⊕E(y)或者 x+y=D(E(x)⊕E(y))成立,並且不泄漏 x 和 y。
乘法同態,如果存在有效算法 ,E(x×y)=E(x) E(y)或者 xy=D(E(x) E(y))成立,並且不泄漏 x 和 y。
混合乘法同態,如果存在有效算法 ,E(x×y)=E(x) y 或者 xy=D(E(x) y)成立,並且不泄漏 x。
減法同態,如果存在有效算法○- ,E(x-y)=E(x)○- E(y)或者 x-y=D(E(x)○- E(y))成立,並且不泄漏 x 和 y,則稱 E 為減法同態。
除法同態,如果存在有效算法○/ ,E(x/y)=E(x)○/ E(y)或者 x/y=D(E(x)○/ E(y))成立,並且不泄漏 x 和 y,則稱 E 為除法同態。
代數同態,如果 E 既是加法同態又是乘法同態。
算術同態,如果 E 同時為加法同態、減法同態、乘法同態和除法同態。
主要套用
雲計算、電子商務、物聯網、移動代碼等。