同一原理(principle of identity)亦稱同一法則,是相對同一概念而顯現的一種關係。一個命題的條件和結論都惟一存在,它們所指的概念是同一概念時,這個命題與其逆命題等效,同一原理是同一法的根據,根據這一原理,對於符契約一原理的命題,就可通過證明其逆命題來確定原命題成立。
基本介紹
- 中文名:同一原理
- 外文名:principle of identity
- 所屬學科:邏輯學
- 別名:同一法則
- 簡介:相對同一概念而顯現的一種關係
基本介紹
同一原理的套用
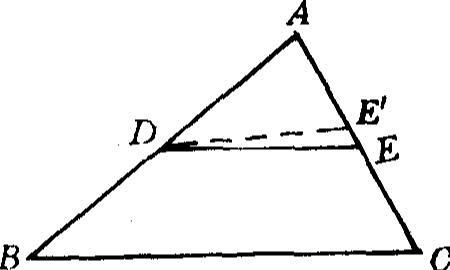
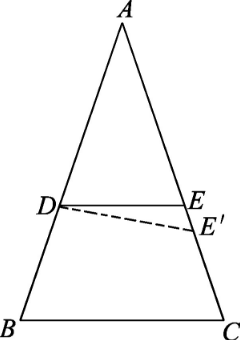

同一原理(principle of identity)亦稱同一法則,是相對同一概念而顯現的一種關係。一個命題的條件和結論都惟一存在,它們所指的概念是同一概念時,這個命題與其逆命題等效,同一原理是同一法的根據,根據這一原理,對於符契約一原理的命題,就可通過證明其逆命題來確定原命題成立。


同一原理(principle of identity)亦稱同一法則,是相對同一概念而顯現的一種關係。一個命題的條件和結論都惟一存在,它們所指的概念是同一概念時,這個命題與其逆命題等效,同一原理是同一法的根據,根據這一原理...
《歸結為同一原理的美的藝術》是一本2022年商務印書館出版的圖書,作者是[法]夏爾·巴托。內容簡介 《歸結為同一原理的美的藝術》於1746年在巴黎首次出版。這本書在藝術史和美學史上具有重要意義,其中將詩、繪畫、雕塑、音樂、舞蹈、演講術及建築等統稱為“美的藝術”,認為它們遵循同一原理,即都是對美的自然之...
(5)效益同一原理要求經濟效益和社會效益並重 經濟效益是效益表現的最直接的形態。任何一個企業都是為了追求一定程度上的營利才進行投入產出活動的。另一方面,我們不能無視社會效益,即不能為營利忽視環境保護,要積極地、義不容辭地處理“三廢”,保護環境,不能為了經濟效益生產假冒偽劣產品,進行不正當競爭,不...
相似原理詳述 相似第一定理 兩個相似的流動現象都屬於同一類物理現象,它們都應為同一的數學物理方程所描述。流動現象的幾何條件(流場的邊界形狀和尺寸)、物性條件(流體密度、粘性等)、邊界條件(流場邊界上物理量的分布,如速度分布、壓強分布等),對非定常流動還有初始條件(選定研究的初始時刻流場中各點的物理...
同一性是指矛盾的對立面相互之間不可分割的聯繫,是對立面之間相互聯結、相互吸引、相互滲透的傾向。 同一性是指兩種事物或多種事物能夠共同存在,具有同樣的性質。生物信息學中,同一性是指兩序列在同一位點核苷酸或胺基酸殘基完全相同的序列比例。同一問題 邏輯中的“同一”問題是“同一性的可替換原理”能否成立的...
原理 同一:從哲學上講,就是表示事物或現象同其自身相等、相同、一樣的範疇。同一認定:是指具有偵查中需要的專門知識和了解偵查客體特徵的人,通過比較偵查客體先後出現的特徵確定是否同一的認識活動。概念 同一認定是依據客體特徵來判斷兩次或多次出現的客體是否為同一個客體的認識活動。同一認定是人類認識客觀事物的...
如果該條件成立,則可以使用疊加原理。這就意味著由在同一空間中傳播的兩個或多個波的合成振幅,是由每個波單獨產生的振幅之和。例如,兩個相向傳播的波將徑直互相穿過,在另一邊不會有任何變形(見最上面的圖)。波干涉 主條目:干涉 波之間的干涉即基於此想法。當兩個或更多波在同一個空間中傳播,在每一點的...
組合原理,是指事物的整體或部分迭加的原理,相關操作加以組合。具體描述 (1)在空間上,將相同的物體或相關操作加以組合;(2)在時間上,將相同或相關的操作進行合併。理論歸納與闡述 (1)組合原理在運用中並不是簡單的疊加,應滿足兩個條件。(1)不同技術因素構成具有統一結構與功能的整體;(2)組合物應該具有新穎...
交換機擁有一條高頻寬的背部匯流排和內部交換矩陣,在同一時刻可進行多個連線埠對之間的數據傳輸。交換機的傳輸模式有全雙工,半雙工,全雙工/半雙工自適應。原理 交換機是根據網橋的原理髮展起來的,學習交換機先認識兩個概念:衝突域 衝突域是數據必然傳送到的區域。HUB是無智慧型的信號驅動器,有入必出,整個由HUB組成...
這相當於把6個東西放入5個抽屜,至少有2個東西在同一抽屜里。抽屜原理的一種更一般的表述為:“把多於kn+1個東西任意分放進n個空抽屜(k是正整數),那么一定有一個抽屜中放進了至少k+1個東西。”利用上述原理容易證明:“任意7個整數中,至少有3個數的兩兩之差是3的倍數。”因為任一整數除以3時餘數只有0...
這與一般飛機的發動機安裝於機首,恐屬同一原理。但人無羽翼,若無強勁的內氣與地心引力相抵斥,則難以在空中作片刻停留,更談上不凌空飛行。此為頂功練法不如內家輕功之處,所謂鐵錫碑,即用錫瓦鐵衣附於身上,按一整套的程式練功。本來人身重於空氣不知有多少倍,為何反加上許多重物而求身法的輕靈呢?這是...
同異反是趙克勤在集對分析中根據對立同一的哲學原理,在常見的同異性思維基礎上給出的一個概念(見文獻[1-3])。基本信息 同異反是趙克勤在集對分析中根據對立同一的哲學原理,在常見的同異性思維基礎上給出的一個概念(見文獻[1-3])。同,泛指同一、協同、等同、相同等.按集對分析,就是指組成集對H的2個...
相似理論,是說明自然界和工程中各相似現象相似原理的學說。是研究自然現象中個性與共性,或特殊與一般的關係以及內部矛盾與外部條件之間的關係的理論。在結構模型試驗研究中,只有模型和原型保持相似,才能由模型試驗結果推算出原型結構的相應結果。理論特點 相似理論主要套用於指導模型試驗,確定“模型”與“原型”的相似...
壓電陶瓷也廣泛用於日常生活中。用了兩個直徑3毫米、高5毫米的壓電陶瓷柱取代了普通的火石製成的氣體電子打火機,可連續打火幾萬次。利用同一原理製成的電子點火槍是點燃煤氣爐極好的用具。還有一種用壓電陶瓷元件製作的兒童玩具,比如在玩具小狗的肚子中安裝壓電陶瓷製作的蜂鳴器,玩具都會發出逼真有趣的聲音。隨著...
廣義相對論(General Relativity) 是描述物質間引力相互作用的理論。其基礎由阿爾伯特·愛因斯坦於1915年完成,1916年正式發表。這一理論首次把引力場等效成時空的彎曲。2022年9月,廣義相對論核心原理獲最精確檢驗 。概念介紹 黑洞 廣義相對論在天體物理學中有著非常重要的套用:它直接推導出某些大質量恆星會終結為一個...
化學平衡是指在巨觀條件一定的可逆反應中,化學反應的正、逆反應速率相等,反應物和生成物各組分濃度不再改變的狀態。可用ΔGₘ=Σνμ=0判斷,μ是反應中A物質的化學勢。根據勒夏特列原理,如一個已達平衡的系統被改變,該系統會隨之改變來抗衡該改變。化學平衡是—種動態平衡。一般用可逆反應中正反應速率和逆...
“它們剩下的只是同一的幽靈般的對象性,只是無差別的人類勞動的單純凝結,即不管以哪種形式進行的人類勞動力耗費的單純凝結。這些物現在只是表示,在它們的生產上耗費了人類勞動力,積累了人類勞動。這些物,作為它們共有的這個社會實體的結晶,就是價值——商品價值。”於是,我們可以得出結論:交換價值是價值的表現...
他首先注意到了被稱之為(弱)等效原理的實驗事實:引力質量與慣性質量是相等的。這一事實也可以理解為,當除了引力之外不受其他力時,所有質量足夠小(即其本身的質量對引力場的影響可以忽略)的測驗物體在同一引力場中以同樣的方式運動。既然如此,則不妨認為引力其實並不是一種“力”,而是一種時空效應,即物體...
方程的同解原理:⒈方程的兩邊都加或減同一個數或同一個等式所得的方程與原方程是同解方程。⒉方程的兩邊同乘或同除同一個不為0的數所得的方程與原方程是同解方程。整式方程:方程的兩邊都是關於未知數的整式的方程叫做整式方程。分式方程:分母中含有未知數的方程叫做分式方程。一元一次方程 只含有一個未知數...
