合比性質是數學分數計算中常用的性質之一,屬於合分比性質中的三大性質之一(包括合比性質、分比性質和合分比性質)。主要運用於三角函式等計算。
基本介紹
- 中文名:合比性質
- 外文名:Equivalence property
- 所屬學科:數學
- 套用:三角函式等計算
原理簡介,推導過程,相關性質,習題舉例,
原理簡介
在一個比例里,第一個比的前後項的和與它後項的比,等於第二個比的前後項的和與它的後項的比,這稱為比例中的合比定理,這種性質稱為合比性質。
用字母表達為:若a/b=c/d,則(a±kb)/b=(c±kd)/d(b≠0、d≠0)
推導過程
當b≠0且d≠0時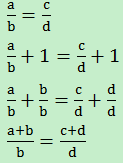 書寫版推導表達
書寫版推導表達
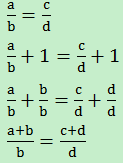 書寫版推導表達
書寫版推導表達a/b=c/d
a/b±k=c/d±k
a/b±kb/b=c/d±kd/d
(a±kb)/b=(c±kd)/d
相關性質
分比性質:
在一個比例里,第一個比的前後項的差與它的後項的比,等於第二個比的前後項的差與它們的後項的比。
字母表達:若a/b=c/d,則(a-b)/b=(c-d)/d (b≠0、d≠0)
在一個比例里,第一個比的前後項的和與它的前後項的差的比,等於第二個比的前後項的和與它的前後項的差的比。
字母表達:若a/b=c/d,則(a+b)/(a-b)=(c+d)/(c-d)(a≠b,c≠d,b≠0,d≠0)
等比性質:
若a1/b1=a2/b2=a3/b3=...=an/bn
則a1/b1=a2/b2=...=(a1+a2+a3+...+an)/(b1+b2+b3+...+bn)=an/bn
習題舉例
如圖,在△ABC中,AD為∠BAC的角平分線,EF是AD的垂直平分線且交AB於E,交BC的延長線於F,求證:DC·DF=BD·CF分析: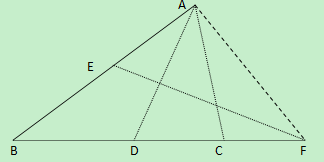 例題圖
例題圖
 例題圖
例題圖欲證:DC·DF=BD·CF
即證:DC/CF=BD/DF
即證:(DC+CF)/CF=(BD+DF)/DF (等式兩邊加上1)
若連結AF,則AF=DF
故即證:AF/CF=BF/AF
只需證△FAB∽△FCA
證明:
連結AF,則AF=DF,∠FAD=∠FDA
∵AD平分∠BAC
∴∠BAD=∠CAD
∴AF=DF
∴∠FDA=∠FAD
又∵∠FAD=∠CAD+∠CAF,∠FDA=∠B+∠BAD
∴∠B=∠CAF
∴△FAB∽△FCA。
