可逆馬爾可夫鏈(reversible Markov chain)是指一種馬爾可夫鏈,指將時間逆向後機率分布律不變的馬爾可夫鏈。
以離散時間參數情形為例.設{X(n),n)叫是一齊次馬爾可夫鏈,其轉移機率矩陣是(產少).如果這鏈是遍歷的,而且初始分布選為平穩分布{二、},於是這馬氏鏈是一平穩序列(這時可以想像鏈早在t=一二已開始,因而在時刻t=。已進人穩定狀態).對任意正整數m,k和任意狀態>}i,iz,…,i*有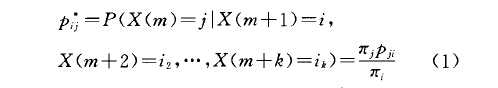
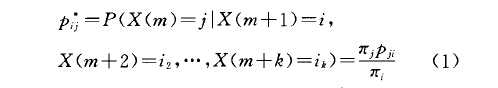
即馬爾可夫鏈{二(}n),n異0}的(關於時間的)逆過程是具有轉移機率矩陣(p}})的馬爾可夫鏈.當對任意i,j有p言= p;,時,就稱這馬爾可夫鏈是(時間)可逆的.從(1)式易知一個(遍歷)馬爾可夫鏈可逆的充分必要條件是對任意i,j有}}p}i-}ipie.
