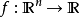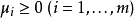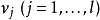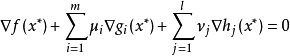在數學中,卡羅需-庫恩-塔克條件(英文原名:Karush-Kuhn-Tucker Conditions常見別名:Kuhn-Tucker,KKT條件,Karush-Kuhn-Tucker最最佳化條件,Karush-Kuhn-Tucker條件,Kuhn-Tucker最最佳化條件,Kuhn-Tucker條件)是在滿足一些有規則的條件下,一個非線性規劃(Nonlinear Programming)問題能有最最佳化解法的一個必要和充分條件。這是一個廣義化拉格朗日乘數的成果。
基本介紹
- 中文名:卡羅需-庫恩-塔克條件
- 外文名:Karush-Kuhn-Tucker Conditions
- 學科:計算機科學
詳解


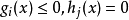
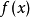


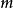
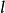
必要條件
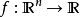



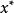
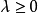

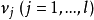


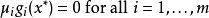
充分條件