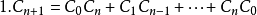簡介 卡特蘭數又稱卡塔蘭數,英文名Catalan number,是
組合數學 中一個常出現在各種計數問題中出現的
數列 。以
比利時 的數學家歐仁·查理·卡塔蘭 (1814–1894)的名字來命名,其前幾項為(從第零項開始) : 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, ...
卡特蘭數Cn滿足以下遞推關係:
歷史 ·1758年,Johann Segner 給出了歐拉問題的遞推關係;
·1838年,研究熱潮:
–GabrielLame給出完整證明和簡潔表達式;
–EugèneCharlesCatalan在研究漢諾塔時探討了相關問題,解決了括弧表達式的問題。
–……
–1900年,EugenNetto在著作中將該數歸功於Catalan。
·1988年以及1999年的文獻研究表明實際上最初發現Catalan數的也不是Euler。
–1753歐拉在解決凸包劃分成三角形問題的時候,推出了Catalan數。
–1730年我國清朝時期的明安圖(蒙古人)比Catalan更早使用了Catalan數,見《割圜密率捷法》。後來他的學生在1774年將其完成發表。
最後由
比利時 的數學家歐仁·查理·卡塔蘭(1814–1894)命名。
原理 令h(0)=1,h(1)=1,catalan數滿足遞推式:
h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)*h(0) (n>=2)
例如:h(2)=h(0)*h(1)+h(1)*h(0)=1*1+1*1=2
h(3)=h(0)*h(2)+h(1)*h(1)+h(2)*h(0)=1*2+1*1+2*1=5
另類遞推式:
h(n)=h(n-1)*(4*n-2)/(n+1);
遞推關係的解為:
h(n)=C(2n,n)/(n+1) (n=0,1,2,...)
遞推關係的另類解為:
h(n)=c(2n,n)-c(2n,n-1)(n=0,1,2,...)
套用 實質上都是遞推等式的套用
括弧化
矩陣連乘: P=a1×a2×a3×……×an,依據乘法結合律,不改變其順序,只用括弧表示成對的乘積,試問有幾種括弧化的方案?(h(n)種)
出棧次序
一個棧(無窮大)的
進棧 序列為1,2,3,…,n,有多少個不同的
出棧 序列?
常規分析
首先,我們設f(n)=序列個數為n的出棧序列種數。(我們假定,最後出棧的元素為k,顯然,k取不同值時的情況是相互獨立的,也就是求出每種k最後出棧的情況數後可用加法原則,由於k最後出棧,因此,在k入棧之前,比k小的值均出棧,此處情況有f(k-1)種,而之後比k大的值入棧,且都在k之前出棧,因此有f(n-k)種方式,由於比k小和比k大的值入棧出棧情況是相互獨立的,此處可用乘法原則,f(n-k)*f(k-1)種,求和便是Catalan遞歸式。ps.author.陶百百)
首次出空之前第一個出棧的序數k將1~n的序列分成兩個序列,其中一個是1~k-1,序列個數為k-1,另外一個是k+1~n,序列個數是n-k。
此時,我們若把k視為確定一個序數,那么根據
乘法原理 ,f(n)的問題就等價於——序列個數為k-1的出棧序列種數乘以序列個數為n - k的出棧序列種數,即選擇k這個序數的f(n)=f(k-1)×f(n-k)。而k可以選1到n,所以再根據
加法原理 ,將k取不同值的序列種數相加,得到的總序列種數為:f(n)=f(0)f(n-1)+f(1)f(n-2)+……+f(n-1)f(0)。
看到此處,再看看卡特蘭數的遞推式,答案不言而喻,即為f(n)=h(n)= C(2n,n)/(n+1)= c(2n,n)-c(2n,n-1)(n=0,1,2,……)。
最後,令f(0)=1,f(1)=1。
非常規分析
對於每一個數來說,必須進棧一次、出棧一次。我們把
進棧 設為狀態‘1’,出棧設為狀態‘0’。n個數的所有狀態對應n個1和n個0組成的2n位
二進制數 。由於等待入棧的運算元按照1‥n的順序排列、入棧的運算元b大於等於
出棧 的運算元a(a≤b),因此輸出序列的總數目=由左而右掃描由n個1和n個0組成的2n位二進制數,1的累計數不小於0的累計數的方案種數。
在2n位二進制數中填入n個1的方案數為c(2n,n),不填1的其餘n位自動填0。從中減去不符合要求(由左而右掃描,0的累計數大於1的累計數)的方案數即為所求。
不符合要求的數的特徵是由左而右掃描時,必然在某一奇數位2m+1位上首先出現m+1個0的累計數和m個1的累計數,此後的2(n-m)-1位上有n-m個 1和n-m-1個0。如若把後面這2(n-m)-1位上的0和1互換,使之成為n-m個0和n-m-1個1,結果得1個由n+1個0和n-1個1組成的2n位數,即一個不合要求的數對應於一個由n+1個0和n-1個1組成的排列。
反過來,任何一個由n+1個0和n-1個1組成的2n位
二進制數 ,由於0的個數多2個,2n為
偶數 ,故必在某一個奇數位上出現0的累計數超過1的累計數。同樣在後面部分0和1互換,使之成為由n個0和n個1組成的2n位數,即n+1個0和n-1個1組成的2n位數必對應一個不符合要求的數。
因而不合要求的2n位數與n+1個0,n-1個1組成的排列一一對應。
顯然,不符合要求的方案數為c(2n,n+1)。由此得出輸出序列的總數目=c(2n,n)-c(2n,n-1)=c(2n,n)/(n+1)=h(n)。
類似問題 買票找零
有2n個人排成一行進入劇場。入場費5元。其中只有n個人有一張5元鈔票,另外n人只有10元鈔票,劇院無其它鈔票,問有多少種方法使得只要有10元的人買票,售票處就有5元的鈔票找零?(將持5元者到達視作將5元入棧,持10元者到達視作使棧中某5元出棧)
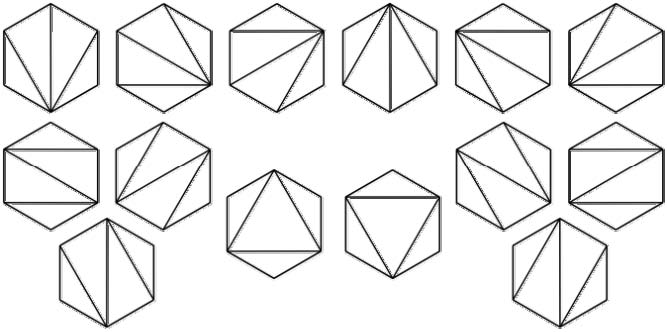
凸多邊形三角劃分
在一個
凸多邊形 中,通過若干條互不相交的對角線,把這個多邊形劃分成了若干個三角形。任務是鍵盤上輸入凸多邊形的邊數n,求不同劃分的方案數f(n)。比如當n=6時,f(6)=14。
分析
如果純粹從f(4)=2,f(5)=5,f(6)=14,……,f(n)=n慢慢去歸納,恐怕很難找到問題的遞推式,我們必須從一般情況出發去找規律。
因為凸多邊形的任意一條邊必定屬於某一個三角形,所以我們以某一條邊為基準,以這條邊的兩個頂點為起點P1和終點Pn(P即Point),將該凸多邊形的頂點依序標記為P1、P2、……、Pn,再在該凸多邊形中找任意一個不屬於這兩個點的頂點Pk(2<=k<=n-1),來構成一個三角形,用這個三角形把一個凸多邊形劃分成兩個凸多邊形,其中一個凸多邊形,是由P1,P2,……,Pk構成的凸k邊形(頂點數即是邊數),另一個凸多邊形,是由Pk,Pk+1,……,Pn構成的凸n-k+1邊形。
此時,我們若把Pk視為確定一點,那么根據
乘法原理 ,f(n)的問題就等價於——凸k多邊形的劃分方案數乘以凸n-k+1多邊形的劃分方案數,即選擇Pk這個頂點的f(n)=f(k)×f(n-k+1)。而k可以選2到n-1,所以再根據加法原理,將k取不同值的劃分方案相加,得到的總方案數為:f(n)=f(2)f(n-2+1)+f(3)f(n-3+1)+……+f(n-1)f(2)。看到此處,再看看卡特蘭數的遞推式,答案不言而喻,即為f(n)=h(n-2) (n=2,3,4,……)。
最後,令f(2)=1,f(3)=1。
此處f(2)=1和f(3)=1的具體緣由須參考詳盡的“卡特蘭數”,也許可從
凸四邊形 f(4)=f(2)f(3)+ f(3)f(2)=2×f(2)f(3)倒推,四邊形的劃分方案不用規律推導都可以知道是2,那么2×f(2)f(3)=2,則f(2)f(3)=1,又f(2)和f(3)若存在的話一定是整數,則f(2)=1,f(3)=1。(因為我沒研究過卡特蘭數的由來,此處僅作劉摶羽的臆測)。
類似問題
一位大城市的律師在她住所以北n個街區和以東n個街區處工作。每天她走2n個街區去上班。如果她從不穿越(但可以碰到)從家到辦公室的對角線,那么有多少條可能的道路?
在
圓上 選擇2n個點,將這些點成對連線起來使得所得到的n條線段不相交的方法數?
給定節點組成二叉搜尋樹
(能構成h(N)個)
(這個公式的下標是從h(0)=1開始的)
n對括弧正確匹配數目
給定n對括弧,求括弧正確配對的字元串數,例如:
0對括弧:[空序列] 1種可能
1對括弧:() 1種可能
2對括弧:()() (()) 2種可能
3對括弧:((())) ()(()) ()()() (())() (()()) 5種可能
那么問題來了,n對括弧有多少種正確配對的可能呢?
考慮n對括弧時的任意一種配對方案,最後一個右括弧有唯一的與之匹配的左括弧,於是有唯一的表示A(B),其中A和B也是合法的括弧匹配序列
假設S(n)為n對括弧的正確配對數目,那么有遞推關係S(n)=S(0)S(n-1)+S(1)S(n-2) +...+S(n-1)S(0),顯然S(n)是卡特蘭數。
擴展 對於在n位的2進制中,有m個0,其餘為1的catalan數為:C(n,m)-C(n,m-1)。證明可以參考標準
catalan 數的證明。
問題1的描述:有n個1和m個-1(n>m),共n+m個數排成一列,滿足對所有0<=k<=n+m的前k個數的部分和Sk > 0的排列數。 問題等價為在一個格點陣列中,從(0,0)點走到(n,m)點且不經過對角線x==y的方法數(x > y)。
考慮情況I :第一步走到(0,1),這樣從(0,1)走到(n,m)無論如何也要經過x==y的點,這樣的方法數為(( n+m-1,m-1 ));
考慮情況II :第一步走到(1,0),又有兩種可能:
a . 不經過x==y的點;(所要求的情況)
b . 經過x==y的點,我們構造情況II.b和情況I的一一映射,說明II.b和I的方法數是一樣的。設第一次經過x==y的點是(x1,y1),將(0,0)到(x1,y1)的路徑沿對角線翻折,於是唯一對應情況I的一種路徑;對於情況I的一條路徑,假設其與對角線的第一個焦點是(x2,y2),將(0,0)和(x2,y2)之間的路徑沿對角線翻折,唯一對應情況II.b的一條路徑。
問題的解就是總的路徑數 ((n+m, m)) - 情況I的路徑數 - 情況II.b的路徑數。
((n+m , m)) - 2*((n+m-1, m-1))
或:((n+m-1 , m)) - ((n+m-1 , m-1))
問題2的描述:有n個1和m個-1(n>=m),共n+m個數排成一列,滿足對所有0<=k<=n+m的前k個數的部分和Sk >= 0的排列數。(和問題1不同之處在於此處部分和可以為0,這也是更常見的情況) 問題等價為在一個格點陣列中,從(0,0)點走到(n,m)點且不穿過對角線x==y的方法數(可以走到x==y的點)。
把(n,m)點變換到(n+1,m)點,問題變成了問題1。
方法數為:
((n+m+1, m)) - 2*((n+m+1-1, m-1))
或:((n+m+1-1, m)) - ((n+m+1-1, m-1))
Java套用 import java.util.*; import java.math.BigInteger; public class Catalan { //求卡特蘭數 public static void main(String[] args){ int numberOfCatalan = 101; //要求多少個卡特蘭數 BigInteger[] digis = new BigInteger[numberOfCatalan]; digis = generateCatalan(numberOfCatalan); Scanner scanner = new Scanner(System.in); int number; while(true) { number = scanner.nextInt(); if(number == -1) break; String answer = digis[number].toString(); System.out.println(answer); } } static BigInteger[] generateCatalan(int numberOfCatalan) { //產生卡特蘭數 BigInteger digis[] = new BigInteger[numberOfCatalan + 1]; BigInteger x = new BigInteger("1"); //第一個卡特蘭數為1 digis[1] = x; int y = 0; int z = 0; for(int counter = 2; counter <= numberOfCatalan; ++ counter) { y = 4 * counter - 2; z = counter + 1; digis[counter] = digis[counter-1].multiply(new BigInteger("" + y)); digis[counter] = digis[counter].divide(new BigInteger("" + z)); } return digis; }} 使用遞歸的方式解決卡特蘭數public static double CatalanNumber(int n) { if (n == 1) { return 1; } else { return CatalanNumber(n - 1) * 2 * (2 * n - 1) / (n + 1); } } public static void main(String[] args) { for (int i = 1; i <= 50; i++) { System.out.println(i + "'s Catalan Number is " + CatalanNumber(i)); } } C++套用 void catalan() //求卡特蘭數{ int i, j, len, carry, temp; a[1][0] = b[1] = 1; len = 1; for(i = 2; i <= 100; i++) { for(j = 0; j < len; j++) //乘法 a[i][j] = a[i-1][j]*(4*(i-1)+2); carry = 0; for(j = 0; j < len; j++) //處理相乘結果 { temp = a[i][j] + carry; a[i][j] = temp % 10; carry = temp / 10; } while(carry) //進位處理 { a[i][len++] = carry % 10; carry /= 10; } carry = 0; for(j = len-1; j >= 0; j--) //除法 { temp = carry*10 + a[i][j]; a[i][j] = temp/(i+1); carry = temp%(i+1); } while(!a[i][len-1]) //高位零處理 len --; b[i] = len; }}