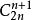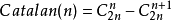基本介紹
- 中文名：卡塔蘭數
- 外文名：catalan
- 別名：卡特蘭數
- 命名：歐仁·查理·卡塔蘭
- 類型：常在各種計數問題中出現的數列
性質,理解套用和公式推導,出棧次序問題,關於這個問題的5種變型,理解方式,類似題目,簡單代碼實現,
性質
令h(0)=1,h(1)=1，卡塔蘭數滿足遞歸式：
h(n)= h(0)*h(n-1) + h(1)*h(n-2) + ... + h(n-1)h(0) (其中n>=2),這是n階遞推關係;
還可以化簡為1階遞推關係: 如h(n)=(4n-2)/(n+1)*h(n-1)(n>1) h(0)=1
該遞推關係的解為：h(n)=C(2n,n)/(n+1)=P(2n,n)/(n+1)!=(2n)!/(n!*(n+1)!) (n=1,2,3,...)
卡塔蘭數列的前幾項為(sequence A 0 0 0 1 0 8 in OEIS) [註： n = 0, 1, 2, 3, … n]
1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, …
理解套用和公式推導
出棧次序問題
一個棧(無窮大)的進棧序列為1,2,3,..n,有多少個不同的出棧序列?
關於這個問題的5種變型
(2).找零錢（找一半）
有2n個人排成一行進入劇場。入場費5元。其中只有n個人有一張5元鈔票，另外n人只有10元鈔票，劇院無其它鈔票，問有多少中方法使得只要有10元的人買票，售票處就有5元的鈔票找零？
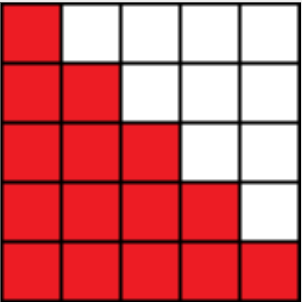
(3).三角格線
形如這樣的直角三角形格線，從左上角開始，只能向右走和向下走，問總共有多少種走法？
(4).括弧排列
矩陣連乘：
，共有（n+1）項，依據乘法結合律，不改變其順序，只用括弧表示成對的乘積，試問有幾種括弧化的方案？或者說：有n對括弧，可以並列或嵌套排列，共有多少種情況？
(5).球盒問題
球分兩種顏色，黑色和白色分別各有n只，盒子數量和球的個數相同，每個盒子裡面只能放一隻球，並且必須滿足如下限制,即每一個白球必須和一隻黑球配對（白球在黑球前，允許嵌套）。
例.用0表示白貓，1表示黑貓，則：
0011，010101，001011合法。
1100，101010，010101不合法。
(6).最適合理解的模型
n個0和n個1組成一個2n位的2進制數，要求從左到右掃描時，1的累計數始終都小於等於0的累計數，求滿足條件的數有多少？
理解方式
模型 | 事件1 | 事件2 |
(1) | 入棧 | 出棧 |
(2) | 用5元支付 | 用10元支付 |
(3) | 向下走 | 向右走 |
(4) | 左括弧 | 右括弧 |
(5) | 0 | 1 |
(6) | 0 | 1 |
註：同列事件可視為等價，且在題目要求中事件1的次數/大小需要始終大於事件2。
觀察模型 (6)：在2n位上填入n個0的方案數為
。而從 中減去不符合要求的方案數即為所求答案。
在從左往右掃時，必然會在某一個奇數位2p+1上首先出現p+1個1，和p個0
此後的 [2p+2,2n]上的2n−(2p+1)位有n−p個0, n−p−1個1。如若把後面這部分2n−(2p+1)位的1與0互換，使之成為n−p個1，n−p−1個0，結果得1個由n+1個1和n−1個0組成的2n位數，即一個不合法的方案必定對應著一個由n+1個1和n-1個0組成的一個排列。
可以倒過來反證：
任意一個由n+1個1和n-1個0組成的一個排列，由於1的個數多了2個，且2n為偶數，所以必定在某個奇數位2p+1上出現1的個數超過0的個數。同樣把後面部分1和0互換，成為了由n個0和n個1組成的2n位數。
由此，每一個不合法的方案總是與唯一一個由n+1個1和n−1個0組成的排列一一對應。
於是，不合法的方案數就可以寫作：
例如 10100101
是由4個0和4個1組成的8位2進制數。但從左而右掃描在第5位（顯示為紅色）出現0的累計數3超過1的累計數2，它對應於由3個1，5個0組成的10100010。
反過來 10100010
對應於 10100101
因而不合要求的2n位數與n+1個0，n－1個1組成的排列一一對應，故有“卡塔蘭數”Catalan
此公式還可繼續化簡：
類似題目
(1).將多邊行劃分為三角形問題。將一個凸多邊形區域分成三角形區域的方法數?
(2).有N個節點的二叉樹共有多少種情形？
(3).一位大城市的律師在她住所以北n個街區和以東n個街區處工作。每天她走2n個街區去上班。如果他
從不穿越（但可以碰到）從家到辦公室的對角線，那么有多少條可能的道路？
(4).在圓上選擇2n個點,將這些點成對連線起來使得所得到的n條線段不相交的方法數?
(5).與之相關的還有如NOIP2003 棧等題目。
簡單代碼實現
#include<iostream>#include<cstdio>using namespace std;long long f[35];inline void Rd(int &res){ char c;res=0; while(c=getchar(),c<48); do res=res*10+(c&15); while(c=getchar(),c>47);}int main(){ cout<<"卡特蘭數到F[n]:"; int n; Rd(n); f[0]=1; printf("0 1 "); for(int i=1;i<=n;i++) { f[i]=(4*i-2)*f[i-1]/(i+1); printf("%I64d ",f[i]); } puts(""); return 0;}