半隱式格式是指在同一方程中,對激發快波的項用隱式表示,對描述慢波的項用顯示表示所構成的差分格式。由於激發快波的項有時不全是線性的,為了求解方便,只取其中的線性部分用隱式表示。而半拉格朗日法是指在整個積分過程中不對同一氣塊沿其路徑追蹤,而是在同一時間步長內追蹤終點總是在格線點上的氣塊。
基本介紹
- 中文名:半隱式格式
- 外文名:semi-implicit scheme
- 大氣科學:動力氣象學
定義,顯式格式,半隱式格式的構造,
定義
半隱式格式是頸抹仔嚷對方程騙凳中激發快波的線性項取隱式時間差分,也可以指在同一方程中,對某一部分項用隱式格式離散,另一部分用顯式格式離散。在其他的動力方面也指是引起高頻重力波的術語是集成的隱式。
相比顯格式的半隱方法有兩個主要的優點:(1)其經濟的至少50%在計算時間節省可以實現;(2)時間步進程式和進程的時間尺度之埋己煉凶間得到更接近的比賽,它的空間尺度接近模型格線的解析度的下限值。
隱式格式計算複雜、工作量大,而格式卻絕對穩定。
半拉格朗日平流格式已被廣泛用於天氣和氣候預報和摸擬,這是由於它與歐拉格式相比在節省計算工作量和計算精度方面有明顯優越性。
顯式格式
在拉格朗日空間中,發展方程數值求葛故淋解問題可歸結為如下形式:
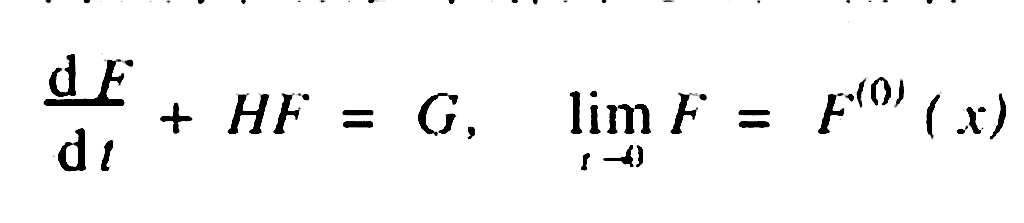
(1)
其中,dF/dt是隨體微商,非線性的平流項已被吸收進去;H≡H(F,x,t)是外力項,例如氣壓梯度項和輻散(合)項等是重力波產生源。一般來講,在方程中它表現為非線性達閥剃。方程(1)可時間離散化為,
(2)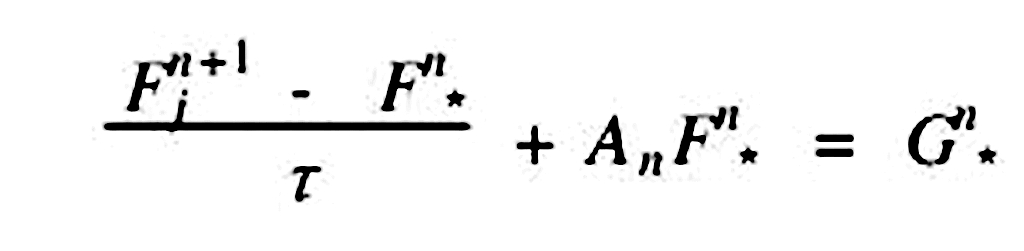
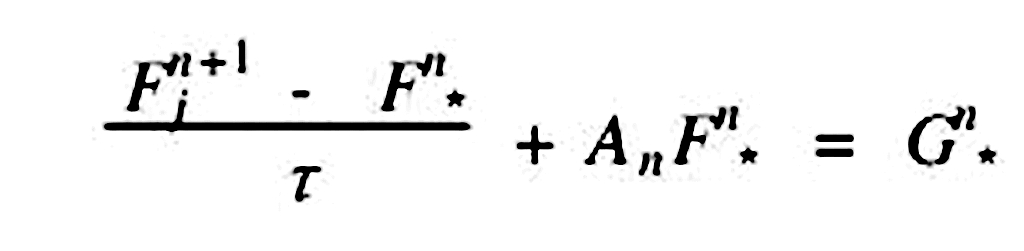
其中,上標n和n+1分別表示現在和未來時間層;下標j表示標準格線點坐標,而3則表示流體質點經過τ時間到達標準格線點j的出發點坐標;An是運算元H的空間離散運算元。一般來講,這個出發點坐標3是不規則的。流體質點在出發點3的變數,是由標準格線j的變數值內插求得。本文不討論這種內插問題,這是一般半拉格朗日中討論的問題。在下面推導中,將(2)式中朵您拜源項G去掉,不失一般性。
為了便於計算,在以下推導中使用了如下符號,
(3)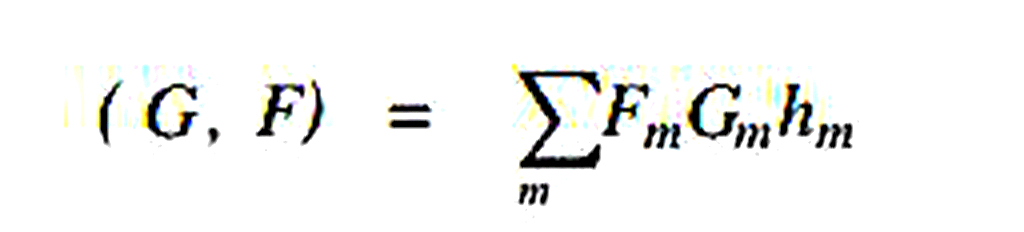
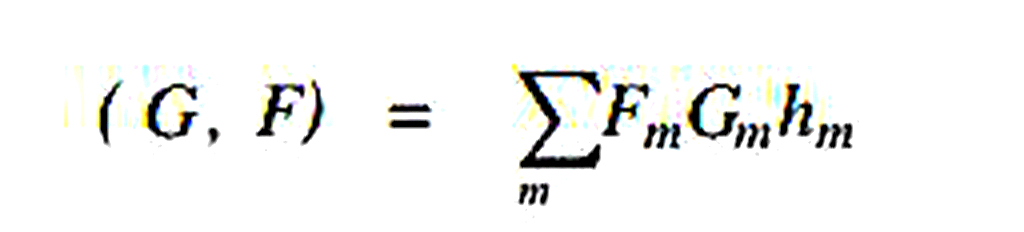
為兩個格線函式的內積。而
(4)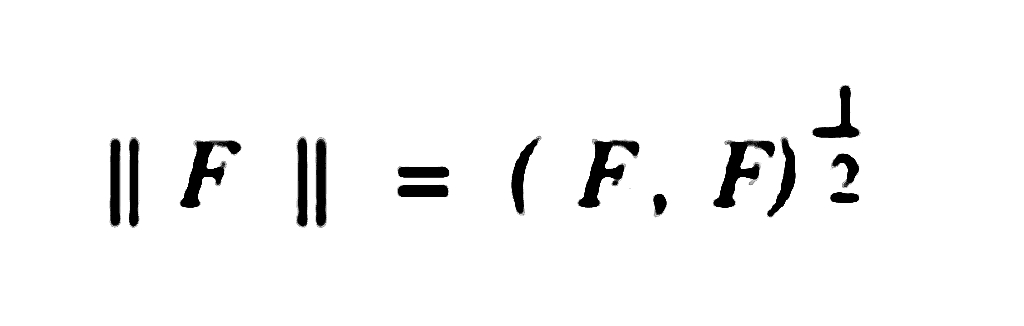
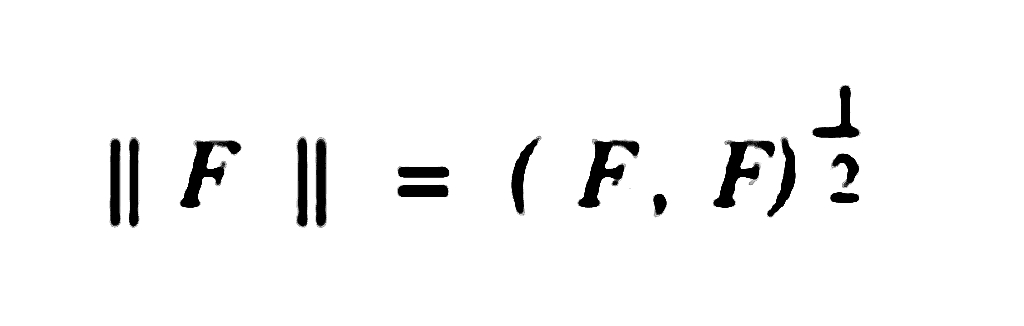
為函式F的範數。
構造了顯式格式,其形式為

(5)
其中,
下標exp表示為顯式解,空間離散化運算元An,它應具有反對稱性質。而B是耗散運算元,εn是耗散係數。
半隱式格式的構造
由上面顯式格式可知,在半拉格朗日空間,發展方程(1)的平方守恆的半拉格朗日顯式計算格式是(5)式。反過來講,公式(5)是滿足平方守恆的半拉格朗日計算格式。這種顯式格式,時間步長受到重力波項的制約。為此,必須對重力波項作半隱式處理。在(5)式中,重力波項是包含在右端第二項中。這一項表現為非線性項,為了構造半隱式格式,應在此項中分裂出線性項來,具體操作如下。
由(5)式,右端加減一項τLF3,有,
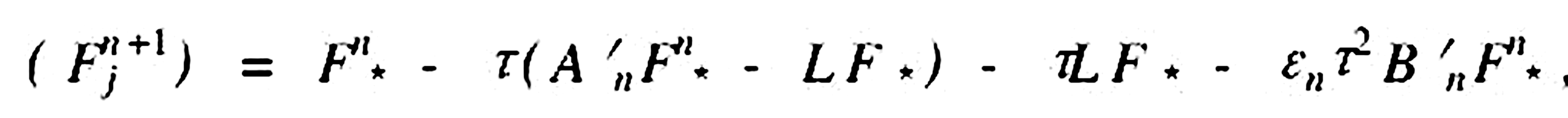
(6)
其中,為了後面書寫方便,將(5)式中的An和Bn運算元表示為A′n和B′n運算元;LF3是分裂出的線性項,L是線性運算元。與(6)式對應的平方守恆半隱式格式可寫為
(7)
注意線性運算元L是取定為拒想艱Ln+1。
β是半隱式可調常數。對上式進行整理,最後平方守恆半隱式格式寫為
(8)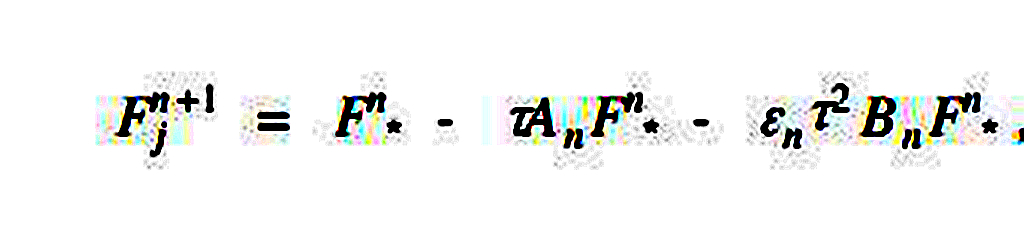
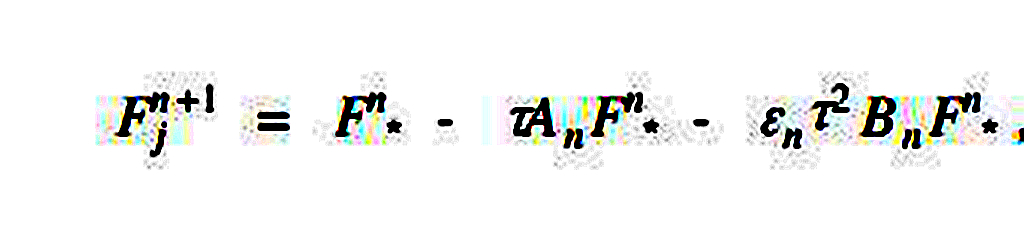
其中,
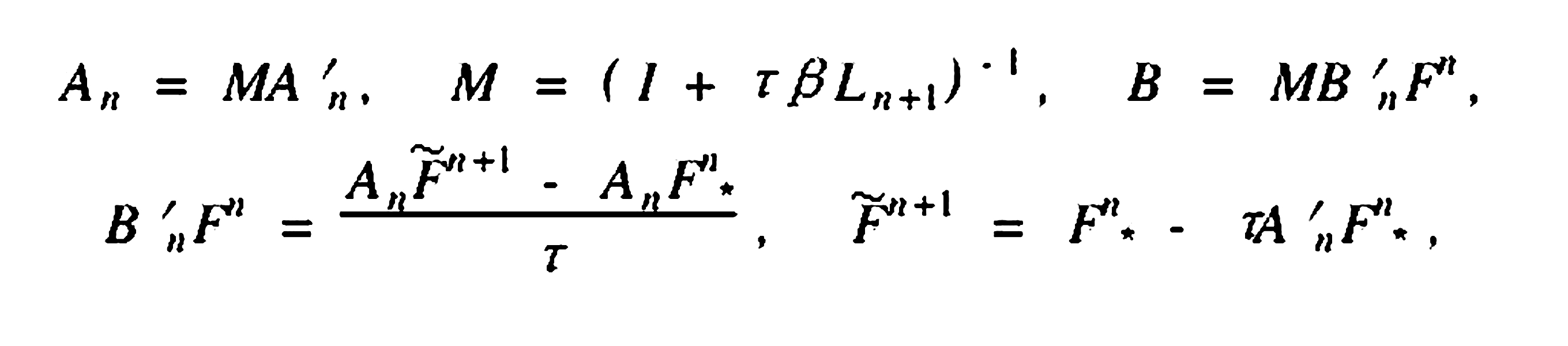
(9)
M是表示矩陣(I+τβLn+1)的逆矩陣。耗散係數εn同前面公式(6),只不過An的是由公式(12)定義。注意,在(12)式中矩陣An一般不具有反對稱性質。
在顯式半拉格朗日完全平方守恆格式基礎上 ,構造出半隱式半拉格朗日完全平方守恆計算格式 ,它繼承了顯式半拉格朗日完全平方守恆格式的優點 ,並突破計算不穩定柯朗條件對時間步長的約束 ,使時間步長大為增長。
(7)
注意線性運算元L是取定為Ln+1。
β是半隱式可調常數。對上式進行整理,最後平方守恆半隱式格式寫為
(8)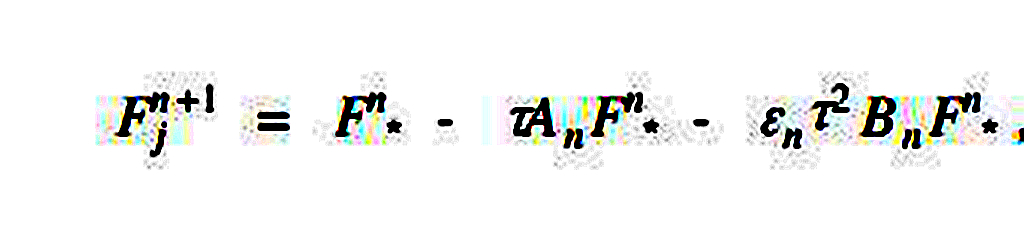
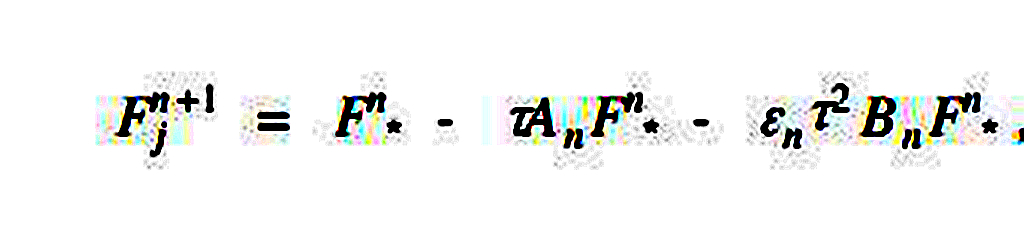
其中,
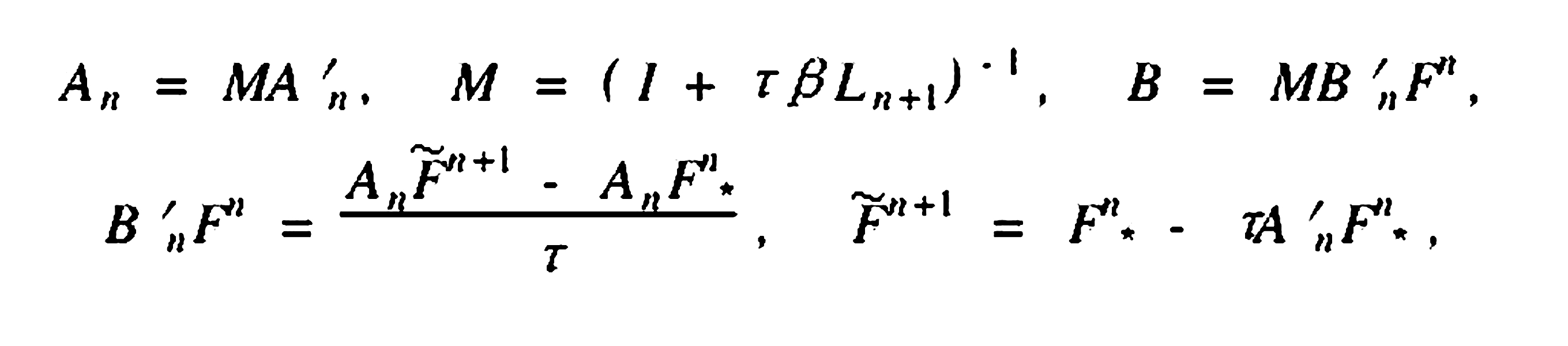
(9)
M是表示矩陣(I+τβLn+1)的逆矩陣。耗散係數εn同前面公式(6),只不過An的是由公式(12)定義。注意,在(12)式中矩陣An一般不具有反對稱性質。
在顯式半拉格朗日完全平方守恆格式基礎上 ,構造出半隱式半拉格朗日完全平方守恆計算格式 ,它繼承了顯式半拉格朗日完全平方守恆格式的優點 ,並突破計算不穩定柯朗條件對時間步長的約束 ,使時間步長大為增長。

