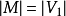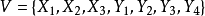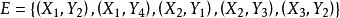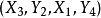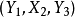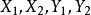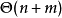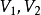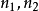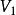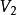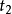基本介紹
- 中文名：匈牙利算法
- 外文名：Hungary
- 提出者：Edmonds
- 提出時間：1965
- 算法的核心：尋找增廣路徑
簡介,概念,複雜度,樣例程式,
簡介
如果一個匹配中，
且匹配數
，則稱此匹配為完全匹配，也稱作完備匹配。特別的當
稱為完美匹配。
概念
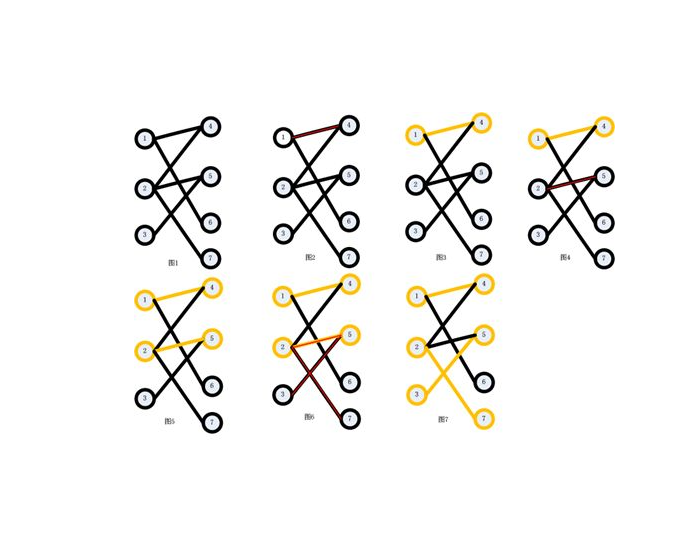
在介紹匈牙利算法之前還是先提一下幾個概念，下面M是G的一個匹配。
若
，
，其中邊
已經在匹配M上。
M-交錯路：p是G的一條通路，如果p中的邊為屬於M中的邊與不屬於M但屬於G中的邊交替出現，則稱p是一條M-交錯路。如：路徑
，
。
M-飽和點：對於
，如果v與M中的某條邊關聯，則稱v是M-飽和點，否則稱v是非M-飽和點。如
都屬於M-飽和點，而其它點都屬於非M-飽和點。
M-可增廣路：p是一條M-交錯路，如果p的起點和終點都是非M-飽和點，則稱p為M-可增廣路。如
（不要和流網路中的增廣路徑弄混了）。
求最大匹配的一種顯而易見的算法是：先找出全部匹配，然後保留匹配數最多的。但是這個算法的時間複雜度為邊數的指數級函式。因此，需要尋求一種更加高效的算法。下面介紹用增廣路求最大匹配的方法（稱作匈牙利算法，匈牙利數學家Edmonds於1965年提出）。
增廣路的定義（也稱增廣軌或交錯軌）：
若P是圖G中一條連通兩個未匹配頂點的路徑，並且屬於M的邊和不屬於M的邊（即已匹配和待匹配的邊)在P上交替出現，則稱P為相對於M的一條增廣路徑。
由增廣路的定義可以推出下述三個結論：
（1）P的路徑個數必定為奇數，第一條邊和最後一條邊都不屬於M。
（2）將M和P進行取反操作可以得到一個更大的匹配
。
（3）M為G的最大匹配若且唯若不存在M的增廣路徑。
算法輪廓：
（1）置M為空
（2）找出一條增廣路徑P，通過異或操作獲得更大的匹配 代替M
（3）重複（2）操作直到找不出增廣路徑為止
複雜度
空間複雜度 鄰接矩陣：
鄰接表：
樣例程式
格式說明
輸入格式：
第1行3個整數，
的節點數目
,G的邊數m
第2-m+1行，每行兩個整數
，代表
中編號為
的點和
中編號為
的點之間有邊相連
輸出格式：
1個整數ans，代表最大匹配數
鄰接矩陣-C
#include<stdio.h>#include<string.h>int n1, n2, m, ans;int result[101];//記錄V2中的點匹配的點的編號bool state[101];//記錄V2中的每個點是否被搜尋過bool data[101][101];//鄰接矩陣true代表有邊相連void init(){ int t1, t2; memset(data, 0, sizeof(data)); memset(result, 0, sizeof(result)); ans = 0; scanf("%d%d%d", &n1, &n2, &m); for(int i = 1; i <= m; i++) { scanf("%d%d", &t1, &t2); data[t1][t2] = true; } return;}bool find(inta){ for(int i = 1; i <= n2; i++) { if(data[a][i] == 1 && !state[i]) //如果節點i與a相鄰並且未被查找過 { state[i] = true; //標記i為已查找過 if(result[i] == 0 //如果i未在前一個匹配M中 || find(result[i])) //i在匹配M中，但是從與i相鄰的節點出發可以有增廣路 { result[i] = a; //記錄查找成功記錄 return true;//返回查找成功 } } } return false;}int main(){ init(); for(int i = 1; i <= n1; i++) { memset(state, 0, sizeof(state)); //清空上次搜尋時的標記 if(find(i)) { ans++; //從節點i嘗試擴展 } } printf("%d\n", ans); return 0;}鄰接矩陣-pascal
Programhungary;Constmax=100;Vardata:array[1..max,1..max]ofboolean;{鄰接矩陣}result:array[1..max]ofinteger;{記錄當前連線方式}state:array[1..max]ofboolean;{記錄是否遍歷過，防止死循環}m,n1,n2,i,t1,t2,ans:integer;Function dfs(p:integer):boolean;vari:integer;beginfor i:=1 to n2 doif data[p,i]and not(state[i]) then{有邊存在且沒有被搜尋過}beginstate[i]:=true;if (result[i]=0)or dfs(result[i]) then{沒有被連過或尋找到增廣路}beginresult[i]:=p;exit(true);end;end;exit(false);end;beginreadln(n1,n2,m);fillchar(data,sizeof(data),0);fori:=1 to mdobeginreadln(t1,t2）；data[t1,t2]:=true;end;fillchar(result,sizeof(result),0);ans:=0;fori:=1 to n1 dobeginfillchar(state,sizeof(state),0);if dfs(i) then inc(ans);end;writeln(ans);end.鄰接表-pascal（使用動態鍊表）
（方法基於之前的鄰接矩陣-pascal）
programhungarian_algorithm;//匈牙利算法typenode=^link;//鍊表定義link=recordg:longint;//指向節點next:node;end;varn1,n2,m,a,v1,v2,ans:longint;flag:array[1..1000000]ofboolean;//記錄在main遞歸過程中是否已訪問過，防止死循環nd:array[1..1000000]ofnode;//鄰接表resultt:array[1..1000000]oflongint;//記錄v2中節點的最終匹配於v1中的幾號節點functionmain(wei:longint):boolean;varp:node;beginp:=nd[wei];whilep<>nildobeginifflag[p^.g]{沒有被搜尋過}thenbeginflag[p^.g]:=false;if(resultt[p^.g]=0)or(main(resultt[p^.g])){沒有被連過或原來指向的節點尋找到新的增廣路}thenbeginresultt[p^.g]:=wei;exit(true);end;end;p:=p^.next;end;exit(false)end;procedureaddd(v1,v2:longint);//建立鄰接表過程varp:node;beginnew(p);p^.g:=v2;p^.next:=nd[v1];nd[v1]:=p;end;beginreadln(n1,n2,m);fora:=1tomdobeginreadln(v1,v2);addd(v1,v2);end;ans:=0;fillchar(resultt,sizeof(resultt),0);fora:=1ton1dobeginfillchar(flag,sizeof(flag),true);ifmain(a)theninc(ans);end;writeln(ans);fora:=1ton2doifresultt[a]<>0thenwriteln(resultt[a],'---',a);end.鄰接表-C++
#include<iostream>#include<cstring>using namespace std;//定義鍊表struct link{ int data;//存放數據 link*next;//指向下一個節點 link(int=0);};link::link(int n){ data=n; next=NULL;}int n1,n2,m,ans=0;int result[101];//記錄n1中的點匹配的點的編號bool state[101];//記錄n1中的每個點是否被搜尋過link*head[101];//記錄n2中的點的鄰接節點link*last[101];//鄰接表的終止位置記錄//判斷能否找到從節點n開始的增廣路bool find(const int n){ link*t=head[n]; while(t!=NULL){//n仍有未查找的鄰接節點時 if(!(state[t->data])){//如果鄰接點t->data未被查找過 state[t->data]=true;//標記t->data為已經被找過 if((result[t->data]==0)||//如果t->data不屬於前一個匹配M (find(result[t->data]))){//如果t->data匹配到的節點可以尋找到增廣路 result[t->data]=n;//那么可以更新匹配M'，其中n1中的點t->data匹配n return true;//返回匹配成功的標誌 } } t=t->next;//繼續查找下一個n的鄰接節點 } return false;}int main(){ int t1=0,t2=0; cin>>n1>>n2>>m; for(int i=0;i<m;i++){ cin>>t1>>t2; if(last[t1]==NULL) last[t1]=head[t1]=new link(t2); else last[t1]=last[t1]->next=new link(t2）； } for(int i=1;i<=n1;i++){ memset(state,0,sizeof(state)); if(find(i))ans++; } cout<<ans<<endl; return 0;}鄰接矩陣-C++
#include<iostream>#include<cstring>using namespace std;int map[105][105];int visit[105],flag[105];int n,m;bool dfs(int a){ for(int i=1; i<=n; i++) { if(map[a][i]&&!visit[i]) { visit[i]=1; if(flag[i]==0||dfs(flag[i])) { flag[i]=a; return true; } } } return false;}int main(){ int n1,n2; while(cin>>n1 >>n2 >>m) { n=n1; memset(map,0,sizeof(map)); for(int i=1; i<=m; i++) { int x,y; cin>>x>>y; map[x][y]=1; } memset(flag,0,sizeof(flag)); int result=0; for(int i=1; i<=n1; i++) { memset(visit,0,sizeof(visit)); if(dfs(i))result++; } cout<<result<<endl; } return 0;}