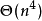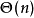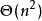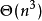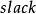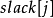KM算法是一種計算機算法,功能是求完備匹配下的最大權匹配。在一個二分圖內,左頂點為X,右頂點為Y,現對於每組左右連線XiYj有權wij,求一種匹配使得所有wij的和最大。
基本介紹
- 中文名:KM算法
- 用途:求的是完備匹配下的最大權匹配
- 基本原理:相等子圖等
- 注意:找匹配時USED都是清0的等
解決思路,基本原理,改進,C/C++代碼,注意,
解決思路
基本原理
該算法是通過給每個頂點一個標號(叫做頂標)來把求最大權匹配的問題轉化為求完備匹配的問題的。設頂點 的頂標為
的頂標為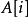 ,頂點
,頂點 的頂標為
的頂標為 ,頂點
,頂點 與
與 之間的邊權為
之間的邊權為 。在算法執行過程中的任一時刻,對於任一條邊
。在算法執行過程中的任一時刻,對於任一條邊 ,
,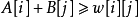 始終成立。
始終成立。

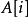






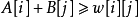
KM算法的正確性基於以下定理:
首先解釋下什麼是完備匹配,所謂的完備匹配就是在二部圖中, 點集中的所有點都有對應的匹配且
點集中的所有點都有對應的匹配且 點集中所有的點都有對應的匹配,則稱該匹配為完備匹配。
點集中所有的點都有對應的匹配,則稱該匹配為完備匹配。


這個定理是顯然的。因為對於二分圖的任意一個匹配,如果它包含於相等子圖,那么它的邊權和等於所有頂點的頂標和;如果它有的邊不包含於相等子圖,那么它的邊權和小於所有頂點的頂標和。所以相等子圖的完備匹配一定是二分圖的最大權匹配。
初始時為了使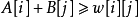 恆成立,令
恆成立,令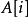 為所有與頂點
為所有與頂點 關聯的邊的最大權,
關聯的邊的最大權, 。如果當前的相等子圖沒有完備匹配,就按下面的方法修改頂標以使擴大相等子圖,直到相等子圖具有完備匹配為止。
。如果當前的相等子圖沒有完備匹配,就按下面的方法修改頂標以使擴大相等子圖,直到相等子圖具有完備匹配為止。
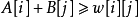
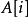


我們求當前相等子圖的完備匹配失敗了,是因為對於某個 頂點,我們找不到一條從它出發的交錯路。這時我們獲得了一棵交錯樹,它的葉子結點全部是
頂點,我們找不到一條從它出發的交錯路。這時我們獲得了一棵交錯樹,它的葉子結點全部是 頂點。現在我們把交錯樹中
頂點。現在我們把交錯樹中 頂點的頂標全都減小某個值
頂點的頂標全都減小某個值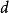 ,
, 頂點的頂標全都增加同一個值
頂點的頂標全都增加同一個值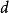 ,那么我們會發現:
,那么我們會發現:



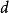

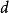
1)兩端都在交錯樹中的邊 ,
, 的值沒有變化。也就是說,它原來屬於相等子圖,現在仍屬於相等子圖。
的值沒有變化。也就是說,它原來屬於相等子圖,現在仍屬於相等子圖。


2)兩端都不在交錯樹中的邊 ,
,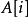 和
和 都沒有變化。也就是說,它原來屬於(或不屬於)相等子圖,現在仍屬於(或不屬於)相等子圖。
都沒有變化。也就是說,它原來屬於(或不屬於)相等子圖,現在仍屬於(或不屬於)相等子圖。

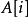

3) 端不在交錯樹中,
端不在交錯樹中, 端在交錯樹中的邊
端在交錯樹中的邊 ,它的
,它的 的值有所增大。它原來不屬於相等子圖,現在仍不屬於相等子圖。
的值有所增大。它原來不屬於相等子圖,現在仍不屬於相等子圖。




4) 端在交錯樹中,
端在交錯樹中, 端不在交錯樹中的邊
端不在交錯樹中的邊 ,它的
,它的 的值有所減小。它原來不屬於相等子圖,現在可能進入了相等子圖,因而使相等子圖得到了擴大。
的值有所減小。它原來不屬於相等子圖,現在可能進入了相等子圖,因而使相等子圖得到了擴大。




5)到最後, 端每個點至少有一條線連著,
端每個點至少有一條線連著, 端每個點有一條線連著,說明最後補充完的相等子圖一定有完備匹配。(若由二分圖中所有滿足
端每個點有一條線連著,說明最後補充完的相等子圖一定有完備匹配。(若由二分圖中所有滿足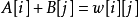 的邊
的邊 構成的子圖(稱做相等子圖)有完備匹配,那么這個完備匹配就是二分圖的最大權匹配。)
構成的子圖(稱做相等子圖)有完備匹配,那么這個完備匹配就是二分圖的最大權匹配。)


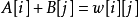

現在的問題就是求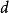 值了。為了使
值了。為了使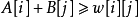 始終成立,且至少有一條邊進入相等子圖,
始終成立,且至少有一條邊進入相等子圖,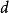 應該等於:
應該等於: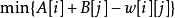 (
( 在交錯樹中,
在交錯樹中, 不在交錯樹中)。
不在交錯樹中)。
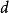
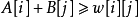
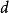
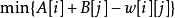


改進
Kuhn-Munkres算法流程:
(1)初始化可行頂標的值;
(2)用匈牙利算法尋找完備匹配;
(3)若未找到完備匹配則修改可行頂標的值;
(4)重複(2)(3)直到找到相等子圖的完備匹配為止。
C/C++代碼
const int N = 20, inf = 2147483647;int w[N][N], linky[N], visx[N], visy[N], lack;int lx[N] = {0}, ly[N] = {0}; //頂標bool find(int x) { visx[x] = true; for (int y = 0; y < N; ++y) { if (visy[y]) continue; int t = lx[x] + ly[y] - w[x][y]; if (!t) { visy[y] = true; if (!~linky[y] || find(linky[y])) { linky[y] = x; return true; } } else lack = min(lack, t); } return false;}void km() { memset(linky, -1, sizeof(linky)); for (int i = 0; i < N; ++i) for (int j = 0; j < N; ++j) lx[i] = max(lx[i], w[i][j]); //初始化頂標 for (int x = 0; x < N; ++x) for (; ;) { memset(visx, 0, sizeof(visx)); memset(visy, 0, sizeof(visy)); lack = inf; if (find(x)) break; for (int i = 0; i < N; ++i) { if (visx[i]) lx[i] -= lack; if (visy[i]) ly[i] += lack; } }}KM算法和最大匹配(匈牙利算法)
2010.7.18
匈牙利算法的分析與運用:
匈牙利算法的精髓在於USED哈希數組的使用,下面是匈牙利算法的主要模組:
function find(x:longint):boolean;var kkk, i, j:longint;begin for j := 1 to m do if (line[x,j]) and (not used[j]) then begin used[j] := true; if (mm[j]=0) or (find(mm[j])) then begin mm[j] := x; exit(true); end; end; exit(false);end;
在原程式進行調用是也就是簡簡單單的一句話:
for i := 1 to n dobegin fillchar(used, sizeof(used), 0); if find(i) then inc(all);end;
注意
匈牙利算法解題是極為簡單的,但是圖論的難並不是難在解答,而是建圖的過程,也難怪會有牛曰:用匈牙利算法,建圖是痛苦的,最後是快樂的。當然,我們這些蒟蒻也只能搞搞NOIP了,一般不會太難,所以此算法,極為好用。
KM算法:
最大流的KM算法,又算的上算法世界中的一朵奇葩了。
解決最大流問題可以使用“網路流”,但較為繁瑣,沒有KM來得痛快,
下面是KM算法的核心模組:
function find(x:byte):boolean;var y:byte;begin find := false; vx[x] := true; for y := 1 to n do if (not vy[y]) and (lx[x] + ly[y] = w[x,y]) then begin vy[y] := true; if (aim[y] = 0) or (find(aim[y])) then begin aim[y] := x; exit(true); end; end;end;
可以見出,該模組與匈牙利算法極為相似,差別便是:
if (not vy[y]) and (lx[x] + ly[y] = w[x,y])
判斷語句了,這裡涉及到KM算法的思想,不再贅述,請自行百度之。
但是源程式的調用過程煩雜:
for k := 1 to n dorepeat fillchar(vx, sizeof(vx), 0); fillchar(vy, sizeof(vy), 0); if (find(k)) then break; d := maxn; for i := 1 to n do if (vx[i]) then for j := 1 to n do if (not vy[j]) then d := min(d, lx[i] + ly[j] - w[i,j]); for i := 1 to n do begin if (vx[i]) then dec(lx[i], d); if (vy[i]) then inc(ly[i], d); end;until false;