包容關係

包容關係即集合之間元素的從屬關係，也稱包含關係，稱集合B包容A，記為A⊆B，若且唯若A的元素必為B的元素。包容關係構成組合理論的基本序關係。因為它本身可以構造出典型的組合形態如布爾代數B(2^E，⊆)，同時藉助於它可以刻畫更為複雜的關係。

基本介紹

• 中文名：包容關係
• 外文名：relation of inclusion
• 所屬學科：數學（集合論）
• 別稱：包含關係
• 簡介：集合之間元素的從屬關係

基本介紹

設f和g均為從集合N到集合M的映射，若只關心N中有多少元素，而不理會是哪些元素映入到它們的像域時，則其像域g(b)可表示為

im(f)={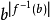|b∈M}，

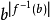
im(g)={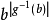|b∈M}.

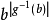
這樣在映射f，g之間建立包容關係：f⊆g若且唯若對M的所有元素b均有|f^-1(b)|≤|g^-1(b)|。

定義

包容關係也稱包含關係，包含是集合與集合之間的從屬關係，也叫子集關係。基本含義近同於蘊含、蘊涵、包涵，關係形容詞。出自漢·桓寬《鹽鐵論·地廣》：“王者包含並覆，普愛無私，不為近重施，不為遠遺恩。”。

設A和B是兩個集合，若集合A的元素都是集合B的元素，則稱集合B包含集合A，或集合A包含於集合B，記作

A⊆B或B⊇A.

分類

（1）包含於（包含）；

（2）真包含（真包含於）。

性質

集合的包含關係有如下性質：設A，B，C為任意三個集合，有

①A⊆A(反身性)；

②若A⊆B，則B⊇A(對稱性)；

③若A⊆B，B⊆C，則A⊆C(傳遞性)，圖1直觀地表示了這一性質。

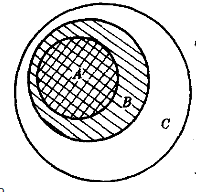圖1