勾股容方是古代中國數學中的一個命題。出自《九章算術》第九卷《勾股》章第十五題。
基本介紹
- 中文名:勾股容方
- 表達式:長度X= HL/(H+L)
- 套用學科:數學
- 出自:《九章算術》
勾股容方是古代中國數學中的一個命題。出自《九章算術》第九卷《勾股》章第十五題。
在均輸章中,他提出了“課分法”、“減分法”,以及用“方程術”求差率的方法;在盈不足章中,他提出了“今有術”、“合率術”、“分率術”、“方程術”、“兩不足術”等方法;在“勾股容方”問中,他提出“勾股旁要法”...
一、勾股容方、容圓問題/166 二、一次測望問題/168 三、重差/168 四、製圖六體/174 第五章 出入相補原理/176 第一節 冪、多邊形和勾股問題/176 一、冪——面積的定義/176 二、多邊形的面積/177 三、解勾股形/178 四、勾股...
卷上包括“割圓弧矢”、“新設三角法”、“方田雜法”、“推秦氏方斜求圓算草”及“堆垛”等條目;卷中是若干勾股“難題”,涉及到勾股和較、勾股冪、勾股邊冪相求、勾股容方、勾股中長、勾股不同式等方面;卷下是“解方補問...
第三節面積、體積、勾股與測望 一面積 二體積 三勾股定理與解勾股形 四勾股容方容圓 第四節開方術、正負術、方程術與數列 一開方術 二正負術 三方程術 四等差數列 第三章中國傳統數學理論體系的完成——東漢末至唐中葉的數學 第...
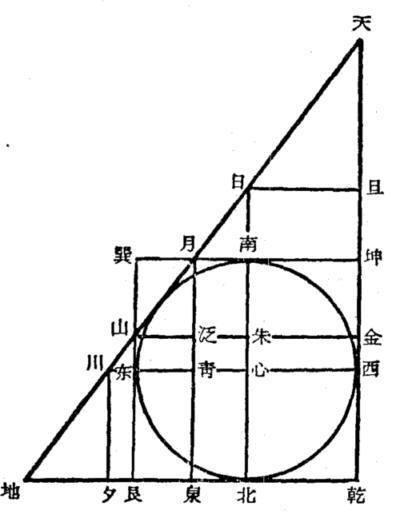
圓城圖式(Yuancheng tushi)中國古算名.指李冶為了利用天元術闡述勾股容方、勾股容圓圖形中的數量關係而設計的一個幾何圖形,其圖如右:假設直角三角形△天地乾的各邊長為680,320,600,從而利用相似比例與勾股定理算出15個直角三角形各邊...
算義探奧(Suanyi tdnao)清代算書.不分卷,清陳厚耀撰.該書分為勾股法義、積求勾股法義、勾股容方容圓法義、三角形求中長法義、測量法義、割圓法義、圓求弧背法義、圓容法義、錯綜法義、推古曆法、推授時曆法、推授時曆...
第二十八卷:勾股,勾股較,勾股和,勾股率,方程入勾股,方求斜。第二十九卷:勾股容方,勾股容圓,圭田容圓,梭田容圓,圓容方,圓套三圓,圓容三角,圓容直,徑矢求弦,滾圓求周。第三十卷 第三十一卷 第三十二卷 第三...
intellectual framework.唐順之(1507年 11月 9日—1560年 4月 25日),字應德,一字義修,號荊川。漢族,武進(今屬江蘇常州)人。明代儒學大師、軍事家、散文家、數學家、抗倭英雄,著有《荊川集》、《勾股容方圓論》等著作。
