簡單來說，這個過程其實是在先擬合出一條曲線，然後再用這個曲線去預測需要預測的點。但是如果這個曲線擬合得不好（或者說樣本數據含有大量噪音），那么這個預測結果就會很差。
基本介紹
- 中文名：加權直線回歸
- 學科：數學
- 性質：名詞
- 特點：預測結果就會很差
局部加權線性回歸,權值的意義,參數學習和非參數學習,參考資料,
局部加權線性回歸
對於一個數據集合(x0,y0),(x1,y1),⋯,(xm,ym)，我們預測它在x點時對應的y值時，如果採用的是傳統的 線性回歸模型，那么：
- Fit θ to mininize ∑i(y(i)−θTx(i))2
- Output θTx
但是對於 局部加權線性回歸(Locally Weighted Linear Regression)來說，在一定程度上可以避免上述問題，但是會付出一些計算量的代價。
局部加權線性回歸(Locally Weighted Linear Regression)的過程是這樣的:
- Fit θ to mininize ∑iw(i)(y(i)−θTx(i))2
- Output θTx
其中w(i)是一個非負的權值，這個權值是用來控制每一個訓練實例對於模型的貢獻，假設要預測的點是x，則w(i)可以定義為:
w(i)=e−(x(i)−x)22τ2(1)
權值的意義
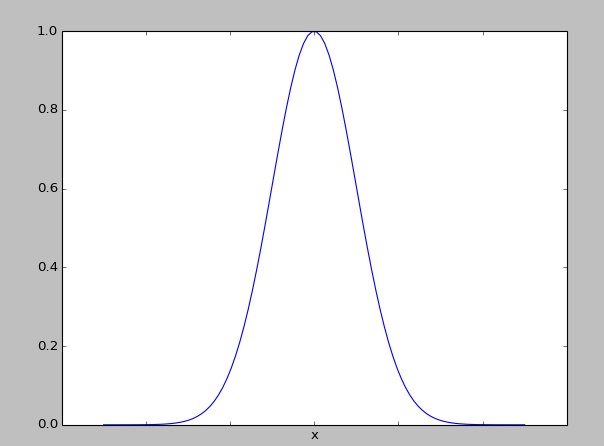
要理解這個憑空多出來的w(i)是什麼意思，我們需要首先來看一下這個函式的圖像:
從圖像中我們可以看到，越是靠近預測點x，其函式值就越接近於1，越是遠離預測點x，其函式值就越接近於0。將這個函式加入到原始的線性回歸模型中，就變成了局部加權線性回歸模型，其直觀意義就是越是靠近預測點的實例點，它們對預測點的影響就應該越大，越是遠離預測點的實例點，它們對預測點的影響就越小，也就是說局部加權線性回歸模型只關注於預測點附近的點(這就是局部的含義)，而不考慮其他遠離預測點的實例點。
參數學習和非參數學習
局部加權線性回歸其實是一個非參數學習算法(non-parametric learning algorithm)，而相對的的，線性回歸則是一個參數學習算法(parametric learning algorithm)，因為它的參數是固定不變的，而局部加權線性回歸的參數是隨著預測點的不同而不同。
由於每次預測時都只看預測點附近的實例點，因此每一次預測都要重新運行一遍算法，得出一個組參數值，因此其計算代價是比較高的。
參考資料
- 斯坦福《機器學習》公開課第三集及其配套講義
