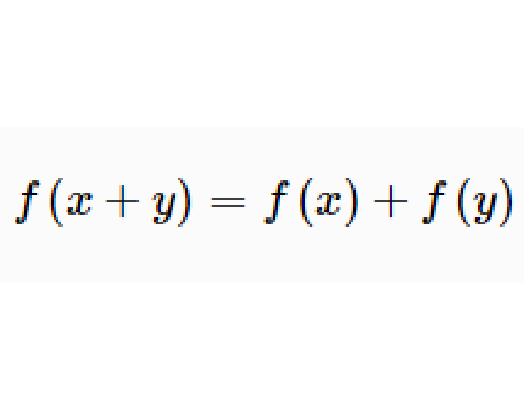基本介紹
形如
的加性函式方程,
柯西(A.-L.Cauchy)證明了方程(1)的連續解只有
(
是常數),即使只要求
在某點連續,在該點鄰域有界或可測,也只有解
。但在非可測函式類中,哈默爾(G.K.W.Hamel)和
勒貝格(H.L.Lebesgue)證明了除
外還有無窮多個解。另一方面,
奧斯特羅格拉茨基(М.В.Остроградский)證明了,如果方程(1)的解
在一個正測度集合上不取兩個相異值之間的值,則
必是連續的。以上結論可以推廣到n個變數的情形。方程(1)的變形方程是
如果存在
使得
,則
恆為零。因此假定
,取
即可看出
,令
,則方程(2)可化為方程(1)。因此,方程(2)的連續解只有
。再考慮方程
如果存在
使得
,則
,因此,假定
時
。對於
,令
,於是方程(3)就化為方程(2),又在方程(3)中取
得到
,所以
,於是方程(3)的連續解是
或
。
一般加法定理
一般加法定理(general addition theorem)是刻畫一種特殊方程存在連續的非零解特徵的一個定理,一般加法定理如下:如果方程
在
中存在連續的非常數解
,那么
必是嚴格單調函式,而
是關於
的嚴格單調遞增連續函式,且
,還存在一個
,使得
,而且關於
中的任意的
,成立恆等式
反之,如果
是具有這些性質的函式,則(4)式存在在
上連續的非常數解,而且若
是這樣的一個解,則
就給出了其他的解,如果
還是連續可微的,則
就是微分方程