剪下變換

剪下變換(shear transformation)是空間線性變換之一，是仿射變換的一種原始變換。它指的是類似於四邊形不穩定性那種性質，方形變平行四邊形，任意一邊都可以被拉長的過程。

基本介紹

• 中文名：剪下變換
• 外文名：Shear transformation
• 屬性：空間線性變換之一
• 相關概念：仿射變換、空間線性變換等

簡介

剪下變換(shear transformation)是空間線性變換之一。變換後的新坐標值如圖1所示，相當於原坐標值經橫向剪下。其中值為剪下常數。剪下變換可以僅是坐標、或僅是坐標受橫向剪下，也可以是兩個坐標同時受橫向剪下。僅坐標受橫向剪下時的變換關係如圖1(b)所示，取決於下式所示的矩陣乘法運算：

僅坐標或坐標受剪下以及與坐標同時受剪下時的變換矩陣分別為：

圖1(a) 剪下變換y向

圖1(b) 剪下變換x向

剪下矩陣

從一系列的旋轉、平移和縮放變換，我們可以得到任意的仿射變換，但是還有一類非常重要的變換——剪下變換，由於該類變換比較重要，所以我們把它當作基本變換，而不是從其他3類變換推導而來。考慮一個處於原點的立方體，該立方體的各表面對齊於各坐標軸，從正軸位置看到的視圖如圖2所示。如果把頂面向右拉而底面向左拉，會得到一個沿軸方向剪下的對象。由於軸和軸方向都不受剪下影響，因此稱該剪下變換為軸剪下，以區別於其他方向的剪下變換。利用圖3中簡單的三角幾何關係，我們發現可以用角度來表示剪下變換的特性。該剪下變換方程為：

從上述3個方程，得到剪下變換矩陣為：

如果沿著相反方向進行剪下變換，則得到剪下的逆變換，因此有

圖2 剪下變換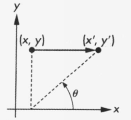

圖3 剪下矩陣的計算過程

通用的3D剪下矩陣

在3D環境下，對象可沿任一坐標軸、任一坐標平面或二者組合實現剪下變換。通用的3D剪下矩陣如下所示：

其中包含了6個剪下參數。該矩陣作用於某一頂點坐標後的效果如下所示：

下面的示例顯示了沿軸方向上的剪下變換且對應的矩陣可表示為：

亦即，根據式(1)，。圖4顯示了一個位於原點處的單位立方體經剪下變換後的效果。

圖4