剛體運動群

保持平面上所有的點之間的距離的平面到自身的映射所構成的群，稱作剛體運動群。不難看出，此種剛體運動群必然把直線映射成直線， 並且保持兩直線的交角不變，理由詳見圖片及正文。

基本介紹

• 中文名：剛體運動群
• 外文名：Rigid Body Motion Group
• 類型：群
• 範圍：群論

定義

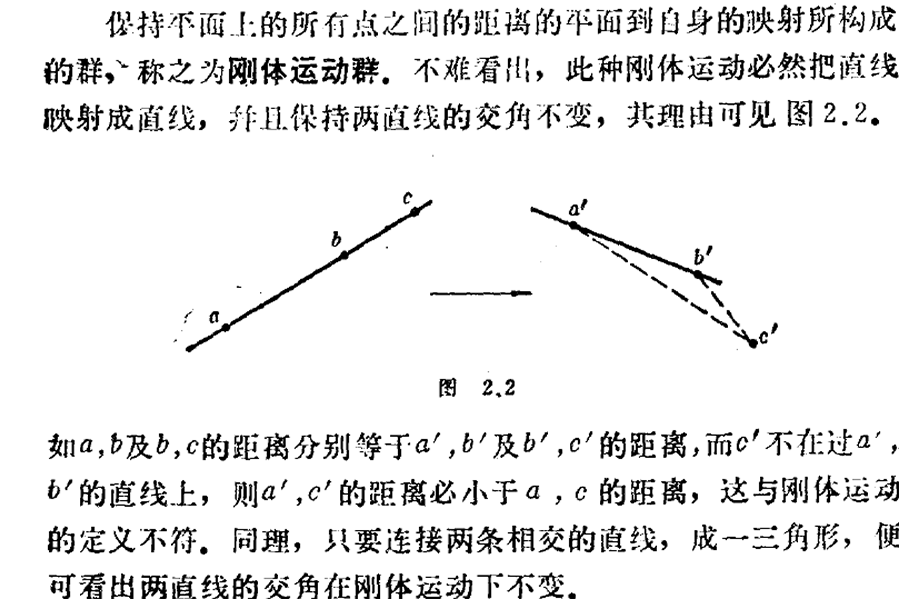
保持平面上所有的點之間的距離的平面到自身的映射所構成的群，稱作剛體運動群。不難看出，此種剛體運動必然把直線映射成直線， 並且保持兩直線的交角不變，理由如下

如a , b及b , c的距離分別等於a ' , b ' 及b ' ,c' 的距離，而c ' 不在過a ' , b'的直線上， 則a'，c' 的距離必小於 a , c 的距離， 這與剛體運動的定義不符．同理，只要連線兩條相交的直線，成一三角形，便可看出兩直線的交角在剛體運動下不變．

物理學常用定義

叉乘（Cross Product）是將兩個三維向量映射到一個三維向量，叉乘可以可以轉化為一個矩陣與向量點乘的形式，方便計算。

剛體運動是三維坐標到三維坐標的映射：

gt:R3→R3;X↦gt(X),t∈[0,T]

t是時刻。

剛體運動保持範數（norm）與叉乘不變：

|gt(v)|=|v|,∀v∈R3

gt(u)×gt(v)=gt(u×v),∀u,v∈R3

由以上兩個性質與極化恆等式（Polarization Identity）可知剛體運動也保持內積不變。三重積（Triple Product）也是保持變不變，三重積的幾何意義是三個向量表示的平行六面體的體積，所以剛體運動保持體積不變。

<gt(u),gt(v)×gt(w)>=<u,v×w>

剛體運動可以表示為：

gt(x)=Rx+T

相關的群

平移群由平移 （ a , b∈ R ）組成， 對平面的 作用定義如下:

( x ,y) = (x + a,y + b).

不難看出

* =

由此可得 是麼元，而 的 逆元素是 .

取平面上的一直線l,對此直線的全體鏡像映射構成一群， 這就是反射群，為簡便起見， 不妨假定這條直線即 是Y 軸， 則鏡像映射如圖2.1所示。鏡象映射γ的作用如下：

圖2.1

γ(x,y) = (-x,y).

不難看出 γ *γ= e（e 表示麼映射，即e ( x , y ) = ( x , y) ）反射群中只有兩個元素 e 及γ 。

平面上以一點為旋轉心的所有旋轉構成一群，即所謂旋轉群．為簡便起見，不妨假定此旋轉心即原點．令旋轉角為θ ( 0 ≤θ< 360 ° ) 的旋轉為 ,不難看出

* = ,

其中θa+θb表示對模360 °的主餘數． 在此群中 為麼元

的逆元素是 。

性質

平面上的平移群、反射群、旋轉群及剛體運動群．令{O;X, Y} 為平面上的一直角坐標系， ( x , y ) 為任意點的坐標．此四群中的元素都是平面上的單滿映射，而其雙項運算都是映射的合成．

取一剛體運動m . 設m 把原點( 0 , 0 ) 映成 ( a , b)點 ，則有

( *m)(0,0) = (a,b) = (0,0),

即 * m 不移動原點．取一適當的旋轉角θ, 以旋轉平面使y軸重合，即

* *m(0,y) = (0,y).

此時 x軸或重合，或恰好反方向 ，也即

* * m = e 或 γ* * *m =e.

由此可得

m = * 或 m = * * γ

即任意剛體運動皆是由平移、旋轉及反射生成的．