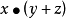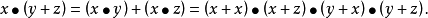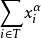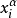初等和亦稱和範式或單因式，是一種特殊的布爾表達式。在初等和中，如果至少有一個變元及其補同時出現，則此初等和恆等於1。
基本介紹
- 中文名：初等和
- 外文名：elementary sum
- 適用範圍：數理科學
定義,初等積,合取範式,
定義
初等和亦稱和範式或單因式，是一種特殊的布爾表達式。
在初等和中，如果至少有一個變元及其補同時出現，則此初等和恆等於1。
初等積
(elementary product)
初等積亦稱積範式或單項式，是一種特殊的布爾表達式。
它由有限個布爾變元或變元的補之積所構成。可寫成
的形式，其中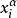
或為xi或為xi'，而T為某有限指標集。在命題代數中，初等積又稱為小項或簡單合取。例如x，x'y，x·y'·z‘均為初等積。初等積是命題代數中簡單合取概念的推廣。
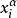
在初等積中，如至少有一個變元及其補同時出現，則此初等積恆等於0。
合取範式
(conjunctive normal form)
合取範式亦稱和積範式或多因式。一種特殊的布爾表達式。
它是有限個初等和之積，可寫成形狀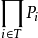
，這裡 Pi 是初等和，T 是有限指標集。任一布爾表達式可通過德 · 摩根律，對合律，分配律及其他布爾代數運算律將其化為合取範式。
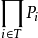
例如
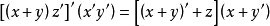
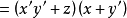
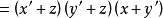
合取範式不是惟一的，例如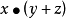
是合取範式，但它亦可寫成
