初相

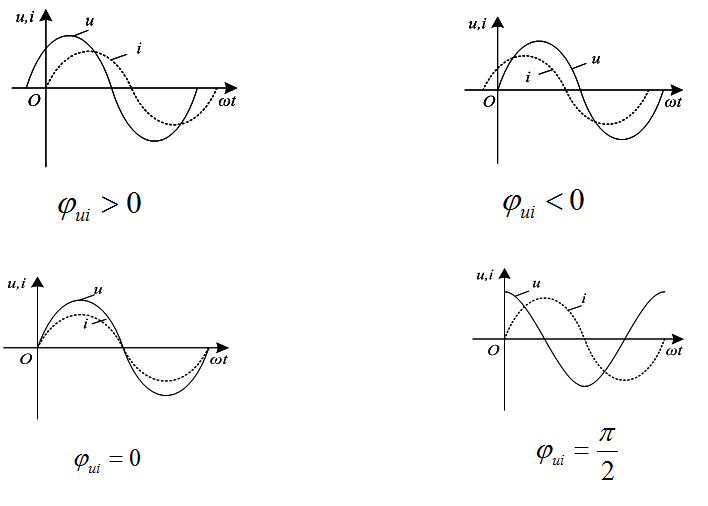
在三角函式y=Asin(ωx+φ) （A>0,ω>0 ）中ωx+φ稱為相位,當x=0時函式y的相位φ就稱為函式y的初相。

基本介紹

• 中文名：初相
• 外文名：initial phase
• 領域：數學
• 運算：代入運算法

初相定義

在三角函式模型中我們會遇到三角函式圖像y=Asin(ωx+φ)。物理中，描述簡諧運動的物理量，如振幅、周期、和頻率等都是與這個解析式中的常數有關。

A就是這個簡諧運動的振幅(amplitude of vibration），它是做簡諧運動的物體離開平衡位置的最大距離；

這個簡諧運動的周期（period）是T=2π/ω，這是做間歇運動的物體往復運動一次所需要的時間；

這個簡諧運動的頻率（frequency)由公式f=1/T=|ω|/2π（這裡的頻率不是指角速率）它是做簡諧運動的物體在單位時間內往復運動的次數；

ωx+φ稱為相位

x=0時的相位（ωx+φ=φ）稱為初相

運算

初相的運算

（1）三角函式圖像向左或向右移動的距離=φ/|ω|（注意移動距離向左符號為正，向右符號為負。謹記左加右減原則）不過這個套用並不廣泛。

（2）帶入運算法：取函式圖像上的某點代入函式表達式即可算出初相φ。

振動方程

振動與波動是醫用物理學的重要內容之一 ，也是其中光學的基礎 .振動方程與波動方程都可用兩種表達式表示：正弦表達式和餘弦表達式。同一狀態，用兩種不同表達式表示 ，其初相值 等均不同。統編教材中振動方程用餘弦表達式而波動方程用正弦表達式 ，但對兩者的區別 與聯繫避而不談 ，極易造成對概念的混亂，同時受課時和專業的限制 ，對兩種形式表示的振動 與波動中的初相也不容易徹底講授清楚 ，針對醫藥院校醫用物理學教學中長期存在的這一問 題可用下述方法解決。

振動方程的初相

由諧振動微分方程 d²s /dt²+ k²s= 0，得出諧振動的振動方程

S = Acos(kt + H) (1) S = Asin(kt + H') (2)

(1)、(2)式都是微分方程的解。根據0時刻的相位為初相，所以H與H'均可為初相。初相的意義是決定質點初始位置與狀態的。H與H'間的關係可由下式導出：

S= Asin(kt+ H' ) = Acos(- kt- H' + c/2)

= Acos(kt+ H' - c/2) = Acos(kt+ H)

H= H' - c/2

正弦可用餘弦表示，反過來餘弦也可用正弦表示，表示形式不同，初相值不同，總是相差c/2。若用餘弦方程中的H定義初相，則正弦方程中的H'不是初相，而是H' - c/2；若用正弦方程中 的H'定義初相，則餘弦方程中的H不是初相，而是H+c /2。這種因方程表示形式不同使質點初相值不同的情況很容易導致對初相概念的混亂，進而對振動和波動也不易理解與掌握.H與 H'究竟那一個表達初相更合適，現從下面三個方面進行論證.

解析法

表1 不同初始狀態下的H與H'值

由表可知，初相為零時，餘弦表達的質點處於"正方向端點"，正弦表達的質點處於"平衡位 置，正方向運動"，表明H的起始位置是"正方向端點"，H'的起始位置是"平衡位置，正方向運 動"，顯然H與H'差值的根本原因是由於兩種表達式的質點起始位置不同而造成的。在一個周 期內，正方向端點只有一個位置，而平衡位置則有兩個位置。由此可知，定義H的參考位置只 需一個條件:正方向端點，而定義H'的參考位置需要兩個條件:①平衡位置，②向正方向運動. 所以解析法表明：H的參考位置比H'的超前c/2,由H比用H'表達初相更簡便;H與H'數值 雖然相差c /2,但其所決定的質點的初相、狀態完全相同。

矢量法

初相H位移S軸正方向與矢量的夾角∠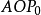 （見圖1）；初相H'：位移S軸正方向沿順時針方向旋轉c/2後與矢量的夾角∠ 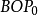（見圖1），或二維直角坐標系（Y軸為位移S軸），X軸的正方向與矢量的夾角為初相∠ 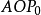（見圖2）。因此，矢量法的結論同上述解析法的結論完全一樣。

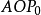
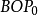
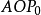
曲線法

初相H與最靠近坐標原點的波峰相對應的 橫軸上的相位值，該點在坐標原點的左邊，初相為 超前（H> 0);右邊為滯後（H <0)(見圖3)。初相 H':在橫軸上最靠近坐標原點的S值為零的相位 值，但必須是該點左邊S值小於零，右邊S值大於零的點;該點在坐標原點的左邊，初相為超前 (H'> 0);右邊為滯後（H'<0)(見圖3)。在一個周期內 ，波峰只有一個，而 S= 0的點有兩個，還必 須再加一個條件：該點左邊S值小於零，右邊S值大於零。因此，曲線法表明的結論同上述解析法、矢量法的結論也完全一樣。

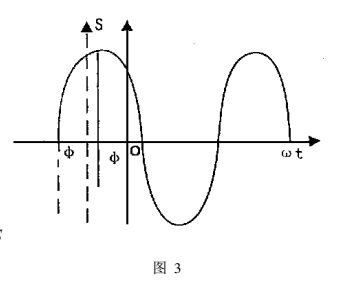圖3

總之 ,解析法、矢量法、曲線法是分析和解決振動與波動問題常使用的方法。因此,建議用H定義振動的初相，即不論正弦表達式還是餘弦表達式，初相是:參考位置是正方向端點(解析法），或位移S軸正方向與矢量的夾角（矢量法），或與最靠近坐標原點的波峰相對應的橫 軸上的相位值 (曲線法 ) 。

波動方程的初相

波動方程由振動方程推導得出.先求波源的振動方程是：S=Acos( kt+ H)，然後推出波沿正方向傳播的波動方程是：S=A cos [k( t - x /c)+ H ] (3)。

不少教材中以波源初相為 -c/2開始計時，測波源的振動方程是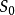： =Acos(kt- c/ 2)= Asinkt，波動方程是： S=A sink( t- x /c) ( 4)，(4)式僅代表波源初相為-c/2時開始計 時的波動方程，作為標準方程初相應取任意值H較好，因此，波動方程的標準式建議用(3)式 表示較好 。

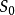
S= Acos[k(t- x/c)+ H] (3)， S= Asin[k(t- x/c)+ H' ] (5)。理論上(3)，(5)式均可作為波動方程，若在振動中不規定H為初相，同樣波動方程中也存在著因表示方式不同而 使波源的初相值不同的問題.若振動用(1)(或(2))式，波動用(5)(或(3))式，其結果振動方程 求出的初相與波動方程求出的初相不相等，總是相差c/2,同樣還是由於H與H'的參考位置 不同其值必然不同.由此看來，波動方程與振動方程的初相不一致時初相也容易發生混亂.解 決這個問題仍然按照振動中定義的H是初相，則不論振動方程還是波動方程，也不論是餘弦 表達式還是正弦表達式，餘弦表示中的H是初相，正弦表示中的H'不是初相，初相是H' - c/ 2.這樣在任何情況求初相都不會引起混亂，一目了然.在(1)、(2)、(3)、(5)表達式中，(1)、(3) 中的H是初相，（2) (5)中的H'不是初相，H'- c/2才是初相.另外需特別注意一點:不論振動方程還是波動方程，餘弦表達式與正弦表達式本質的區別是初相的參考位置的不同.波動方程 由振動方程推出 ，兩者的標準方程應保持一致是指初相的參考位置一致 ，而不是指表達形式一 致.在具體問題中用H定義初相，振動方程與波動方程可用餘弦表達式也可用正弦表達式，以 表達結果最簡單為原則，而不是說振動方程用餘弦表達式(或正弦表達式)，波動方程一定要用 餘弦表達式 (或正弦表達式 )。

距波源為x處的質點的初相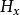 由波源的初相H(或H' )及波源到該質點的距離x決定。

=H- kx/c= H- 2x/λ(或 ' = H' - kx /c= H+ c/2- kx /c= H+c/2- 2cx/λ)若不規定H為初相，同樣也會出現上述問題。

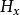
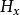
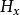
總之，初相在振動與波動中是一個非常重要的概念，用H比用H'表達初相更簡便，也利於 理解初相和掌握振動與波動的規律，並且避免了初相因表達式不同而數值不同的混亂結果等 弊端。