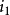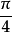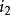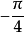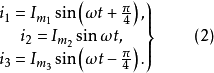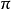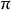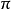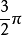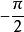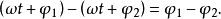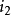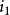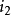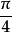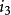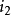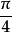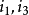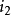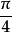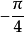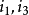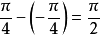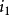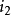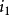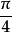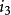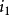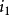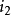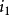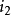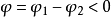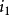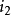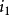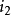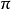基本介紹
如同時研究二個或多個周期變化的交變數,由幅值為零至某一瞬間值所占一個周期中的角度數,就稱為
相角。例如:甲交流量正在增大,但乙交流量卻正在減少。如果取一瞬間來分析,則它們的瞬時值也許是不同的。如圖:當時間是零時,電流
與電流
之瞬時值不同。為了說明這種現象,可用相位表示。電流
在循環剛開始時(或者說
的時間),與我們研究的某一瞬間(t=0的時間)相差多少,以角度表示,即為此
的初相角。一個周期相當於360°角(即
角)。如圖,
之初相角是
,
之初相角是
。但如果我們研究的瞬間改為剛好是
時,則
之初相角是零,但
之初相角則為
。所以初相角是相對的,比較的,用它可以說明若干個交流量的循環起始位置。
初相角又可用矢量表示,
與橫軸所夾的角為
之初相角
,
與橫軸所夾的角為
之初相角
。
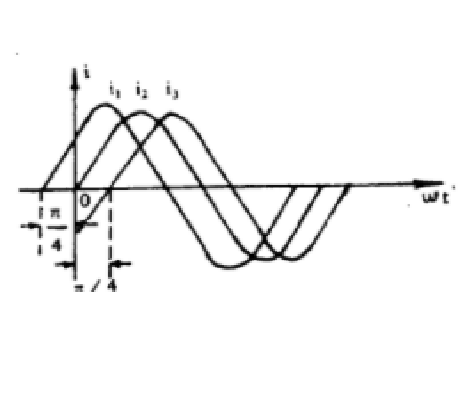
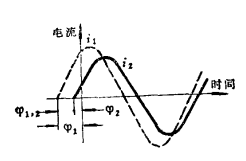 圖1 初相角的波形圖
圖1 初相角的波形圖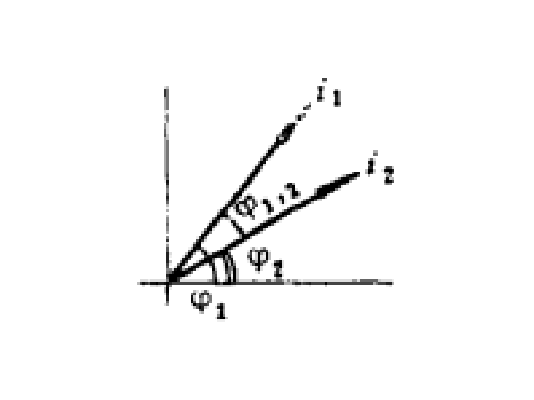 圖2 初相角的矢量圖
圖2 初相角的矢量圖注意點
(1)初相角通常是在180°的範圍內取值,相位差也在該範圍內取值。初相角用角度或
弧度表示均可。
(2)凡是同頻率的任意兩個
正弦量,不管是兩個電壓還是兩個電流,或者是一個電壓一個電流,都可以討論它們的相位關係。頻率不同的兩個正弦量,因它們沒有確定的相位差,所以討論它們之間的相位差是沒意義的。
(3)相位差與計時起點的選擇無關。因為當兩個同頻率正弦量的計時起點改變時,它們的初相角也隨之改變。但兩者的相位差仍保持不變。
相關概念
相位差
兩個正弦交流電它們的振幅和角頻率完全相同,但是初相角
不同,我們不能說這兩個正弦交流電完全相同。正弦交流電的初相角不相同,反映兩個正弦交流電在相位上的不同,初相角對分析正弦交流電是非常重要的。如果兩個振幅和頻率相同的正弦交流電流初相角也相同,則兩電流相加振幅增大一倍,如果初相角相差
,則兩電流完全反相,相加後互相抵消,合成電流為零。
初相角是指在t=0時的正弦交流電的相位角,兩個不同初相角的交流電流可以表示為:
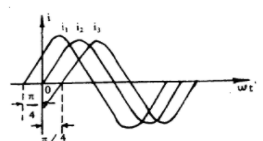 圖3不同初相角的正弦電流
圖3不同初相角的正弦電流實際上初相角與時間的起點選擇有關,時間起點不同初相角也不同。t=0時,函式值為零,則初相角為零;函式值為正,初相角為正;函式值為負,初相角為負。圖3表示三種不同初相角的交流電流,其中
的初相角為
,
的初相角為零,
的初相角為
,它們的瞬時值分別為:
習慣上初相角不用大於
的角來表示,當初相角大於
時可化成小於
的負角表示。例如超前號
可用
來表示。
為了比較兩個同頻率的正弦交流電的相位關係,引入相位差的概念。兩個同頻率的正弦交流電相位之差叫做相位差。式(1)中的兩個電流相位差為:
這說明兩個同頻正弦交流電的相位差等於它們初相角之差,而與角頻率
及時間
沒有關係,通常把初相角為零的正弦量叫做
參考正弦量。在圖3中,
為參考正弦電流,
比
的相位超前
,
比
的相位落後
,因此
與參考電流
的相位差分別為
和
,而
之間的相位差為
。
實際上,參考正弦量的選擇是任意的。例如在圖1中,選
為參考電流,則
比
落後
,
比
落後
。它們之間的相位差不因參考電流的改變而變化。
相位差與交流量的關係
從以上討論可以看出,相位差實際上說明兩個正弦量在時間上的超前或滯後的關係。如果
,則說明
超前
,即
的最大值出現時刻比
早φ,如果
,則說明
滯後
,電流
的最大值出現比
滯後一個φ角。
相位差為零的兩個正弦交流電稱為
同相,相位差為
的兩個正弦交流電稱為
反相,相位差為
的兩個正弦交流電稱為
正交。
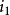
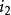
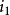
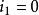
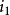
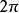
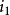
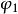

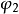
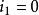
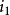

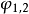
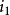
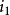
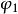


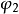
 圖1 初相角的波形圖
圖1 初相角的波形圖 圖2 初相角的矢量圖
圖2 初相角的矢量圖
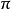
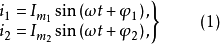
 圖3不同初相角的正弦電流
圖3不同初相角的正弦電流