基本介紹
- 中文名:切爾諾夫限
- 外文名:Chernoff bound
- 分類:計算機 數學
- 別名:切爾諾夫不等式
- 類似:馬爾科夫限 切比雪夫限
- 引申:絕對誤差 相對誤差
定義,證明,示例,絕對誤差(加法形式),相對誤差(乘法形式),套用,
定義
切爾諾夫限,也稱為切爾諾夫不等式,是關於一組獨立隨機變數和的一類機率不等式.。是由赫爾曼-切爾諾夫而命名的。然而,切爾諾夫約束要求變數是獨立的,而與之相類似的馬爾科夫限和切比雪夫限都不需要。
證明
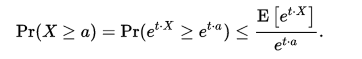
當是n個隨機變數 的時候,我們得到任何
的時候,我們得到任何 ,
,


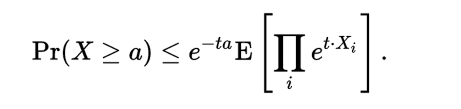
最佳化 並使用
並使用 獨立的假設,
獨立的假設,


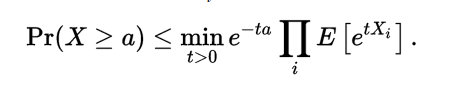
同樣的,
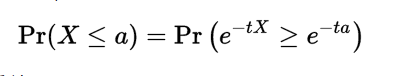
所以,
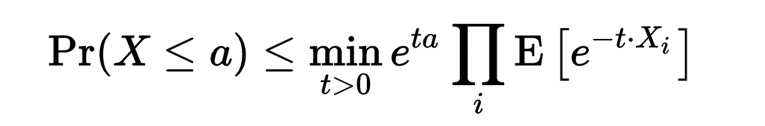
命題得證,以上不等式的一個重要意義在於,我們僅僅知道隨機變數的數字特徵便可以得到機率的界。
示例
令X1,...,Xn是獨立的伯努利隨機變數,其總和為X,每個都具有等於1的機率p> 1/2。對於伯努利變數,
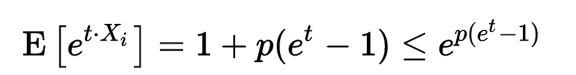
所以,
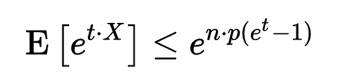
對於任何的 ,由
,由 和
和 可得,
可得,



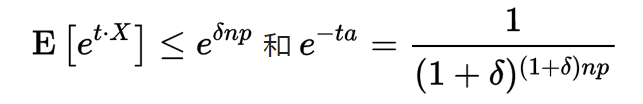
利用切爾諾夫不等式可得,
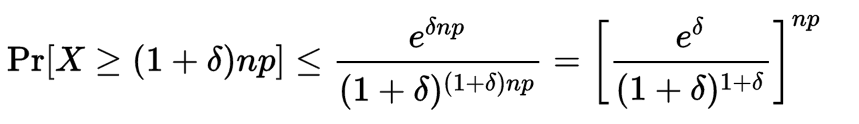
同時發生事件 的
的 以上的機率具有精確的值,
以上的機率具有精確的值,


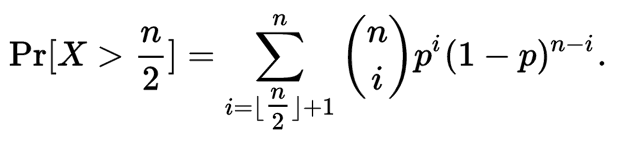
這個機率的下限通過切爾諾夫不等式來計算,
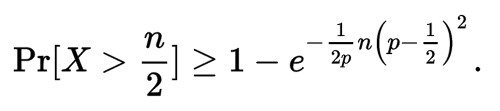
最後得出,
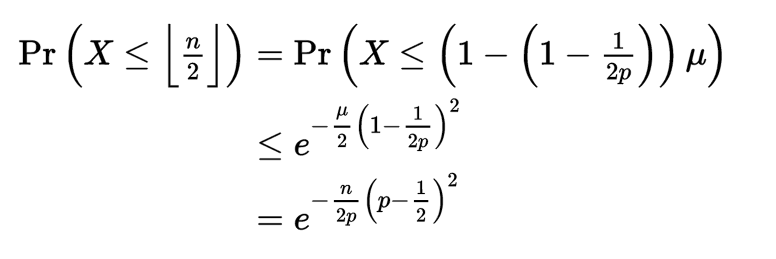
絕對誤差(加法形式)
以下定理是瓦西里·霍夫丁提出的,所以稱為切爾諾夫-霍夫丁定理。
假設X1,...,Xn是隨機變數,取{0,1}中的值。令p = E [ X i ],ε > 0。然後,
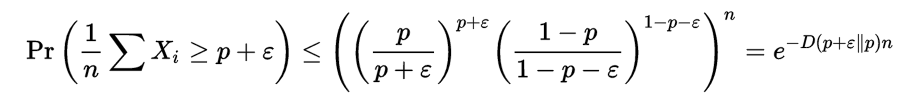
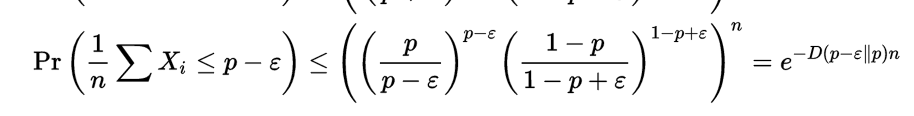
由於,
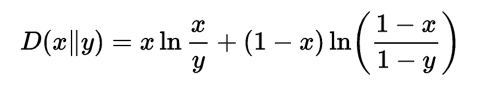
所以
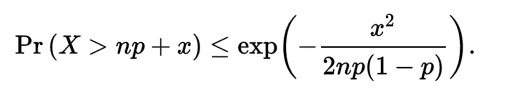
相對誤差(乘法形式)
假設X1,...,Xn是隨機變數,取{0,1}中的值。令X表示他們的和, 表示和的預期值,對於任何
表示和的預期值,對於任何 ,
,


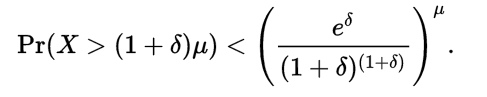
類似的證明出,
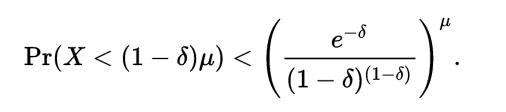
上述公式在實踐中往往不方便,因此常常使用以下更簡單方便的界限:
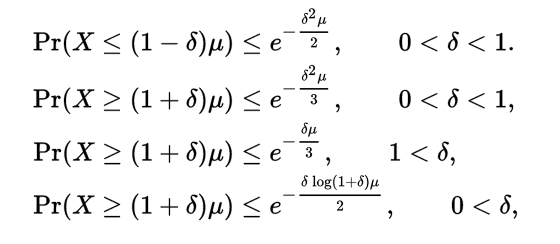
套用
設計統計實驗時出現設定的平衡問題。通常在設計統計實驗時,考慮到實驗中每個參與者的特徵,我們需要知道如何將參與者分成兩個不相交的組,使得每個特徵在兩組之間儘可能大致相等。
切爾諾夫限也用於獲得排列路由問題的緊密界限,在減少網路擁塞的同時稀疏網路中路由數據包。
切爾諾夫限可以有效地用於通過隨機化探索其擾動空間來評估套用算法的“魯棒性”級別。使用切爾諾夫限放棄不切實際的小擾動假設(擾動幅度很小)。魯棒性級別又可以用於驗證或拒絕特定的算法選擇,硬體實現或其結構參數受不確定性影響的解決方案的適當性。



