分配問題(distribution problem)一類組合問題。將n件物分到r個盒子裡,求不同的分配方法數,就構成了分配問題。所求方法數就是分配數。對於物和盒子給定不同的規定條件,可以構成不同的分配問題。
基本介紹
- 中文名:分配問題
- 外文名:distribution problem
- 類別:數學
- 別名:分派問題
- 類屬:最最佳化
- 基本條件:物可辨或不可辨等
- 類型:數學術語
分配問題,二次分配問題,基本條件,
分配問題
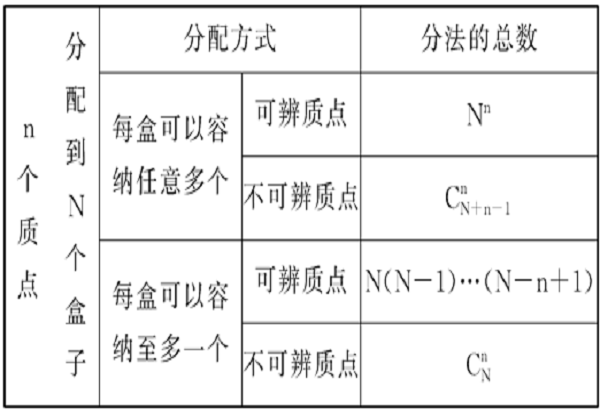
分配問題是一類古典概型問題。即古典概型計算中的分房問題。假設有N個盒子,分別標有號碼1,2,…,N;此外有n個質點。所謂分配問題,就是如何將質點分配到各個盒子裡去,其中n≤N。假設每個質點分配到各個盒中是等可能的,其分配方式和各種分法的總數如下表:
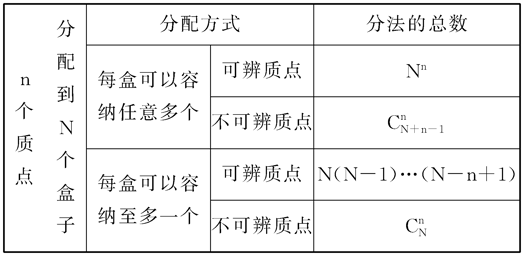
例如,計算下列兩事件的機率:
1.A={某指定的n個盒子中各有一個質點}。
2.B={恰有n個盒子中各有一個質點}。
四種分配方式按上表順序編號:
1.第一種分配方式(又稱麥克斯韋-玻耳茲曼統計):每盒可以容納任意個質點且質點可辨,有
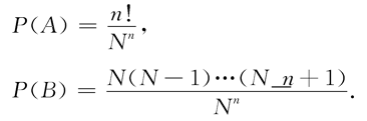
2.第二種分配方式(又稱為鮑澤-愛因斯坦統計):每盒可以容納任意個質點且質點不可辨,有
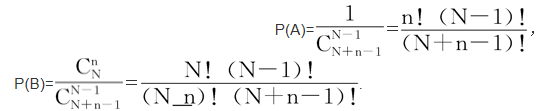
3.第三種分配方式:每盒至多可以容納一個質點且質點可辨,有
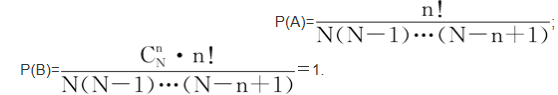
4.第四種分配方式(又稱費米-狄喇克統計):每盒至多可以容納一個質點但質點不可辨,有
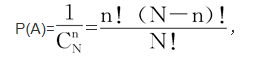
二次分配問題
二次分配問題(quadratic assignment problem, QAP)是最經典,最具有挑戰性的組合最佳化問題之一。自1957年Koopmans和Beckmann首次將QAP問題作為組合最佳化問題提出之後,其已被廣泛套用於諸多領域,許多問題像積體電路布線、工廠位置布局、打字機鍵盤設計、作業調度問題等等,都可形式化為二次分配問題。此外,QAP問題也被套用於統計數據分析、考古數據排序和接力賽跑隊的排序等。另外,一些NP-hard組合最佳化問題,如旅行商問題(the traveling salesman problem),三角剖分問題(triangulation problem)和最大團問題(the max clique problem)等也可以轉化為二次分配問題。基於QAP問題理論和實際的重要性,過去幾十年已激發了許多學者對其理論、套用和最佳化技術的研究。
1976年Sahni和Gonzales證明了QAP不僅屬於NP-hard問題而且不存在近似度的多項式時間近似算法。QAP是很難求解的最最佳化問題,其主要原因是所謂的“組合爆炸”現象,求解時間隨問題規模呈指數增長。一般而言,當問題規模n>20時,很難在有效的計算時間內利用經典算法找到其最優解,如分支定界法、割平面法等。為了實際可行地解決QAP問題,人們退而求其次,許多啟發式算法不斷提出並被套用到QAP的求解,如模擬退火算法、遺傳算法、螞蟻算法、粒子群算法、禁忌搜尋算法和貪婪隨機自適應搜尋算法等。然而,這些啟發式算法不能保證找到的解一定是最優解,他們僅可以在人們可接受的時間內給出較優解。
由於QAP問題高度的計算複雜性和具有代表性的求解難度,許多新的算法,理論和思想在被提出後也常常使用QAP作為測試其自身性能的標準,求解QAP問題已經成為最佳化技術成功的主要體現之一。
基本條件
分配問題的基本條件是:
1.物可辨(相異)或不可辨(相同)。
2.盒子可辨或不可辨。
3.分到盒子裡的物是有序的或無序的。
4.允許有空盒,或不許有空盒。
物和盒子都是不可辨分配也稱為分拆。