分波法是說入射平面波eikz按球面波展開,展開式中的每一項稱為一個分波,每個分波在中心力場的影響下,各自產生一個相移。而的獲得需根據U(r)的具體形式解徑向方程。求出R(r),然後取其漸近解,即可得到第l個分波的相移,由於每個分波都將產生相移,所以,計算散射截面時須尋找各個分波的相移,這種方法稱為分波法。
基本介紹
- 中文名:分波法
- 外文名:Sub-wave method
- 領域:量子力學
- 適用範圍:l≤ka
- 相關名詞:玻恩近似法
簡介,分波法的適用範圍,說明,散射截面,定義,計算,
簡介
分波法是說入射平面波eikz按球面波展開,
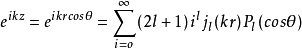
展開式中的每一項稱為一個分波,每個分波在中心力場的影響下,各自產生一個相移 。而
。而 的獲得需根據U(r)的具體形式解徑向方程。
的獲得需根據U(r)的具體形式解徑向方程。



求出R(r),然後取其漸近解,並寫成

即可得到第l個分波的相移,由於每個分波都將產生相移 ,所以,計算散射截面時須尋找各個分波的相移,這種方法稱為分波法。
,所以,計算散射截面時須尋找各個分波的相移,這種方法稱為分波法。

分波法的適用範圍
分波法求散射截面是一個無窮級數的問題。從原則上講,分波法是散射問題的普遍方法。但實際上,依次計算級數中的各項是相當複雜的,有時也是不可能的,所以只能在一定的條件下計算級數中的前幾項,達到一定精確度即可。
散射主要發生在勢場的作用範圍內,若以散射中心為心,以a為半徑的球表示這個範圍,則r>a時,散射效果就可以忽略不計了。
由於入射波的第l個分波的徑向函式 的第一極大值位於
的第一極大值位於 附近,當r較大時,l愈大,
附近,當r較大時,l愈大, 愈快,如果
愈快,如果 的第一極大值位於
的第一極大值位於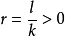 ,即
,即 時,在
時,在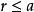 內,
內, 的值很小。亦即第l個分波受勢場的影響很小,散射影響可以忽略,只有第l個分波之前的各分波必須考慮。所以,把分波法適用的條件寫成
的值很小。亦即第l個分波受勢場的影響很小,散射影響可以忽略,只有第l個分波之前的各分波必須考慮。所以,把分波法適用的條件寫成 ,而
,而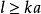 的分波不必考慮,ka愈小,則需計算的項數愈小,當
的分波不必考慮,ka愈小,則需計算的項數愈小,當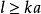 時,
時, ,這時僅需計算一個相移 即足夠了,ka足夠小,意味著入射粒子的動能較低,所以分波法適用於低能散射,
,這時僅需計算一個相移 即足夠了,ka足夠小,意味著入射粒子的動能較低,所以分波法適用於低能散射, 的分波散射截面可以略去。
的分波散射截面可以略去。




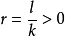

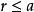


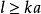
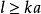



說明
已知U(r)時,可用分波法求出低能散射的相移和散射截面,在原子核及基本粒子問題中,作用力不清楚,也即不知道U(r)的具體形式,這時,我們可先由實驗測定散射截面和相移,然後確定勢場和力的形式和性質,這是研究原子核及基本粒子常用的一種方法。
散射截面
定義
散射截面,描述微觀粒子散射機率的一種物理量。又稱碰撞截面,簡稱截面。一種運動中的粒子碰撞另一種靜止粒子時,如果在單位時間內通過垂直於運動方向單位面積上的運動粒子數為1,靜止粒子數也是1,則單位時間發生碰撞的機率稱為碰撞截面,截面的量綱與面積的量綱相同 ,單位是靶恩,1靶恩=10-28米2,可見與核反應截面的含義相同。如果碰撞為彈性散射,相應的截面稱為彈性截面,如果碰撞為非彈性散射,相應的截面稱為非彈性截面。根據粒子散射截面的分析可獲得許多有關粒子的信息。
計算
設單位時間內散射到(θ,φ)方向面積元ds上(立體角dΩ內)的粒子數為dn,顯然


綜合之,則有:

或

比例係數q(θ,φ)的性質:
q(θ,φj)與入射粒子和靶粒子(散射場)的性質,它們之間的相互作用,以及入射粒子的動能有關,是θ,φ的函式。q(θ,φ)具有面積的量綱,故稱q(θ,φ)為微分散射截面,簡稱為截面或角分布。
如果在垂直於入射粒子流的入射方向取面積q(θ,φ),則單位時間內通過此截面q(θ,φ)的粒子數恰好散射到(θ,φ)方向的單位立體角內。
