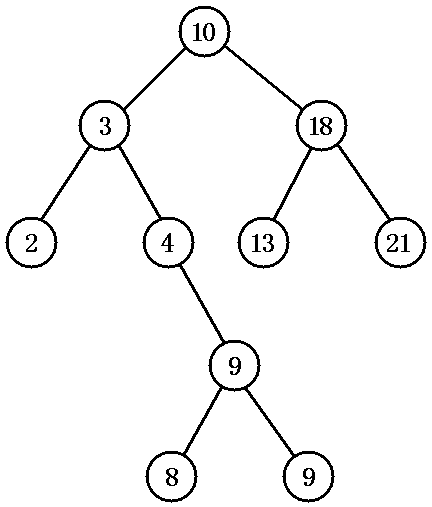
在計算機運算、樹數據結構、博弈論領域中,分支因子(branching factor)是每個結點下的子結點數,即出度。如果各個結點分支因子不同,則可以計算平均分支因子。例如,在西洋棋中,如把一步合法走法算作一個“結點”,那么平均分支因子據信約為35。這表示,棋手每一步走棋平均有大約35種合法走法。相比之下,圍棋的分支因子為250。
基本介紹
- 中文名:分支因子
- 外文名:branching factor
- 學科:計算機科學
- 別名:出度
- 定義:每個結點下的子結點數
- 特性:指數增長
簡介,指數增長,剪枝,
簡介
分支因子有多種解釋,在計算機運算中,分支因子是指從一步運算進行下一步運算有多種選擇。在數據結構中,樹由稱為結點的元素按照層次結構的方式組織而成。層次結構最頂端的結點稱為根。與根結點直接相連的結點稱為根的子結點,通常子結點本身也有屬於它們自己的子結點。除了根結點外,在這個層次體系中的每個結點都有單一的父結點,也就是與其直接相連的上級結點。一個節點擁有多少個子節點取決於樹的類型,這個量值稱為樹的的分支因子,它決定了當插入結點時樹的分支擴展的速度。
一般來說,圖可分為有向圖和無向圖。有向圖的所有邊都有方向,即確定了頂點到頂點的一個指向;而無向圖的所有邊都是雙向的,即無向邊所連線的兩個頂點可以互相到達。在一些問題中,可以把無向圖當作所有邊都是正向和負向的兩條有向邊組成。頂點的度是指和該頂點相連的邊的條數。特別是對於有向圖來說,頂點的出邊條數稱為該頂點的出度,也可稱為分支因子。
因結點數呈指數增長,所以分支因子越大,需要遍歷所有分支的算法(如暴力搜尋法)的計算量越大。例如,若分支因子為10,則當前位置下一層會有10個結點,下兩層會有102即100個結點,下三層會有103即1,000個結點,依此類推。分支因子越大,指數爆炸越快。剪枝算法可以減小分支因子。
指數增長
指數增長(包括指數衰減)指一個函式的增長率與其函式值成比例。在定義域為離散的且等差的情況下,也稱作幾何增長或幾何衰減(函式值是一個等比數列)。或指在某一階段時間內,套用於持續增 長的基數上的不變的增長率。例如,以複利比例增長的儲蓄賬目;越集越 大的雪球;以年平均3%的速度增長的人口等。指數增長模型也稱作馬爾薩斯增長模型。
剪枝
剪枝,就是通過某種判斷,避免一些不必要的遍歷過程,形象的說,就是剪去了搜尋樹中的某些“枝條”,故稱剪枝。套用剪枝最佳化的核心問題是設計剪枝判斷方法,即確定哪些枝條應當捨棄,哪些枝條應當保留的方法。剪枝最佳化三原則: 正確、準確、高效的原則搜尋算法,絕大部分需要用到剪枝。然而,不是所有的枝條都可以剪掉,這就需要通過設計出合理的判斷方法,以決定某一分支的取捨。 在設計判斷方法的時候,需要遵循一定的原則。
正確性
枝條不是愛剪就能剪的。 如果隨便剪枝,把帶有最優解的那一分支也剪掉了的話,剪枝也就失去了意義。 所以,剪枝的前提是一定要保證不丟失正確的結果。
準確性
在保證了正確性的基礎上,我們應該根據具體問題具體分析,採用合適的判斷手段,使不包含最優解的枝條儘可能多的被剪去,以達到程式“最最佳化”的目的。 可以說,剪枝的準確性,是衡量一個最佳化算法好壞的標準。
高效性
設計最佳化程式的根本目的,是要減少搜尋的次數,使程式運行的時間減少。 但為了使搜尋次數儘可能的減少,我們又必須花工夫設計出一個準確性較高的最佳化算法,而當算法的準確性升高,其判斷的次數必定增多,從而又導致耗時的增多,這便引出了矛盾。 因此,如何在最佳化與效率之間尋找一個平衡點,使得程式的時間複雜度儘可能降低,同樣是非常重要的。 倘若一個剪枝的判斷效果非常好,但是它卻需要耗費大量的時間來判斷、比較,結果整個程式運行起來也跟沒有最佳化過的沒什麼區別,這樣就太得不償失了。