分布聚合性指數 aggregation index, disper- sion 群體內個體集中方式(分布方式)的程度,一般稱為分布聚合程度(degree of aggregation)。根據每個區分內個體數的分布頻率提出各種指數作為其衡量尺度。
基本介紹
- 中文名:分布聚合性指數
- 外文名:aggregation index
- 一般簡稱:分布聚合程度
- 衡量尺度:每個區分內個體數的分布頻率
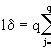
分布聚合性指數 aggregation index, disper- sion 群體內個體集中方式(分布方式)的程度,一般稱為分布聚合程度(degree of aggregation)。根據每個區分內個體數的分布頻率提出各種指數作為其衡量尺度。
分布聚合性指數 aggregation index, disper- sion 群體內個體集中方式(分布方式)的程度,一般稱為分布聚合程度(degree of aggregation)。根據每個區分內個體數的分布...
聚合物和低分子量化合物不同,沒有一個固定的分子量,而是不同分子量同系物的混合體系。因此聚合物分子量是一個平均值,有一個分布的概念。這種分子量的不均一性,...
狄利克雷分布是指數族分布之一,也是劉維爾分布(Liouville distribution)的特殊形式...聚合性(aggregation property)狄利克雷分布具有聚合性,對服從狄利克雷分布的隨機...
鏈長分布chain length distribution對同一聚合物中高分子漣尺寸不一的特性的描述方式。在高分子化學中,常用聚合度的多分散係數(或稱不均勻指數,d'}來表征;在高...
聚丙烯醯胺(PAM)作為一種重要的水溶性高分子材料,在石油化工等領域有著廣泛的...聚合產物進行表征,得到的聚丙烯醯胺的數均分子量為105~106,分子量分布指數DI為 ...
聚乙烯相對分子質量與熔融指數的關係 聚乙烯的相對分子質量分布MWD 聚乙烯的結構特點 聚乙烯的大分子鏈結構 乙烯聚合物的支鏈類別、數量和分布 聚乙烯相對分...
Polymer dispersity index(PDI)是聚合物分散性指數,用於描述聚合物分子量分布。... Polymer dispersity index(PDI)是聚合物分散性指數,用於描述聚合物分子量分布。高...
2 5 2基團數比對聚合度的影響302 6線形縮聚物的聚合度分布322 6 1聚合度分布函式322 6 2聚合度分布指數332 7體形縮聚和凝膠化33...
