共焦有心圓錐曲線族(family of the confocalcentral conics)是一類圓錐曲線的集合。圓錐曲線亦稱圓錐截線。簡稱錐線。一類重要的二次曲線。它是不過圓錐頂點的平面與圓錐面相交而成的曲線。
基本介紹
- 中文名:共焦有心圓錐曲線族
- 外文名:family of the confocalcentral conics
- 領域:數學
- 定義:一類圓錐曲線的集合
- 性質:圓錐曲線
- 坐標:橢圓坐標系
概念,圓錐曲線,曲線族,曲線坐標,
概念
共焦有心圓錐曲線族(family of the confocalcentral conics)是一類圓錐曲線的集合。即以兩定點F,F′為焦點的橢圓以及雙曲線的全體。設焦點坐標為(±c,0),則以t為參數的方程tx+(c+t)y=t(c+t)表示該曲線族,並且橢圓族(t>0)與雙曲線族(0>t>-c)正交。通過各象限內部的點屬於這個曲線族的橢圓及雙曲線各有一個,而且它們是正交的。因而,這個曲線族構成的正交曲線坐標系,稱為橢圓坐標系。
圓錐曲線
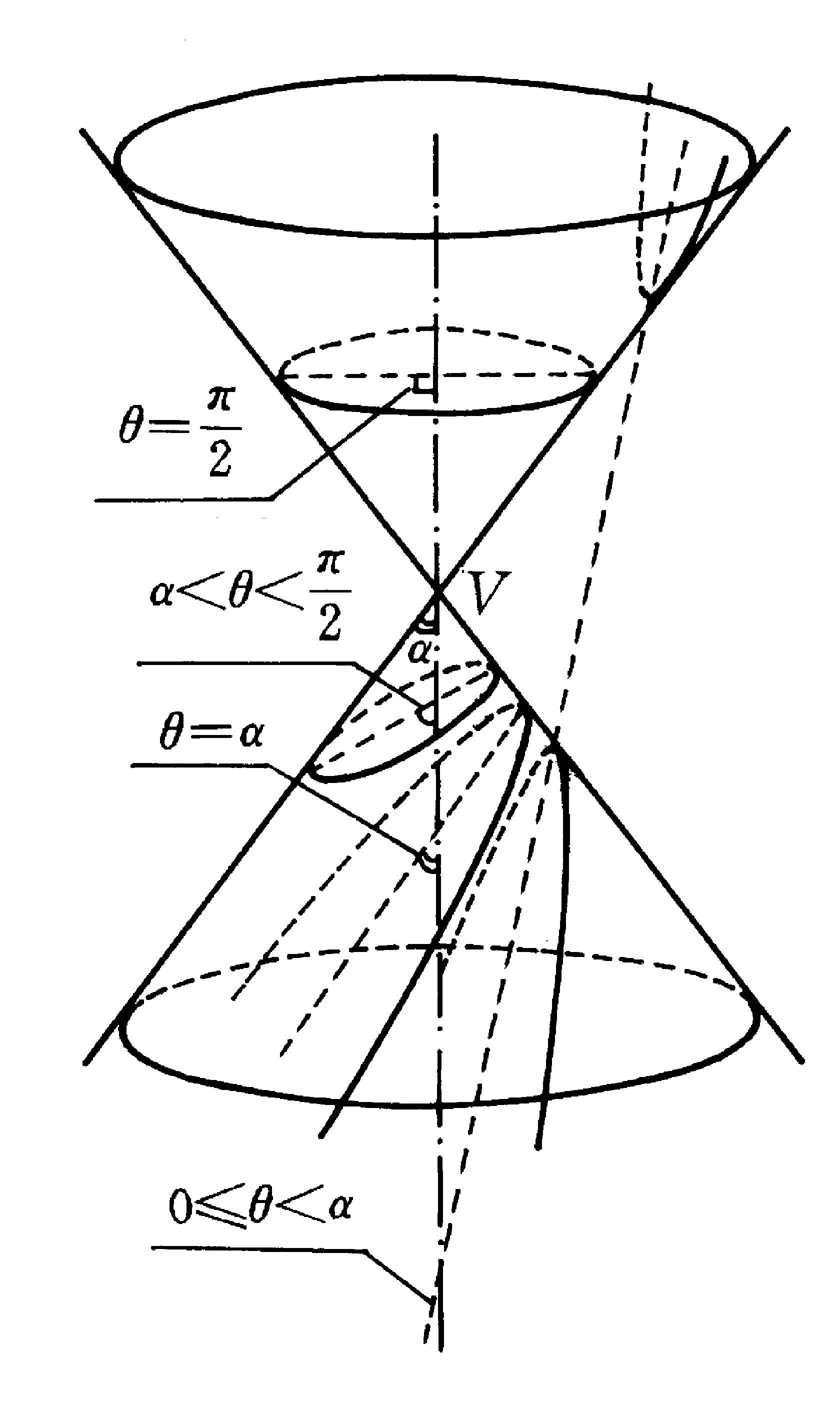
亦稱圓錐截線。簡稱錐線。一類重要的二次曲線。它是不過圓錐頂點的平面與圓錐面相交而成的曲線。設圓錐的半頂角為α,平面與圓錐的軸所成的角為θ。當θ=α時,截面和圓錐的一條母線平行,交線是拋物線;當α<θ≤π/2時,截面和所有的母線相交,交線是橢圓,特別當θ=π/2時,交線是圓;當0≤θ<α時,截面和兩條母線平行,交線是雙曲線。因此,圓錐曲線包括拋物線、橢圓和雙曲線,統稱圓錐曲線。如果平面過圓錐的頂點,截面與圓錐面的交集有以下幾種情況:當θ=α時,平面與圓錐面相切於圓錐的一條母線,可視為退化拋物線;當α<θ≤π/2時,平面與圓錐面有惟一公共點(圓錐的頂點),可視為退化的橢圓;當0≤θ<α時,平面與圓錐面相交於兩條母線,可視為退化雙曲線。這些交集統稱為退化圓錐曲線。一般所謂的圓錐曲線,是指非退化的圓錐曲線。在平面仿射坐標系中,圓錐曲線的方程都是二元二次方程,因此,圓錐曲線又稱為二次曲線。而且平面與任何二次曲面的交線總是二次曲線。例如,圓柱的斜截口即為橢圓。構想在圓錐的頂點V處放一點光源,圓在燈光下的陰影一般是圓錐形的。因此,圓錐曲線是圓在中心投影下,在不同平面上的射影。橢圓、拋物線、雙曲線與圓在中心投影下互變的規律性對於航空測量(高空照片的分析)和透視學研究具有重要意義。
圓錐曲線最早是由古希臘學者梅內克謬斯(Menaechmus)進行系統研究的。他用頂角分別為直角、銳角和鈍角三種直圓錐以不過頂點而垂直一條母線的平面截割這三種圓錐曲面而分別得到拋物線、橢圓和雙曲線的一支.到了亞歷山大里亞時期,阿波羅尼奧斯(Apollonius,(P))在他的《圓錐曲線學》中指出同一圓錐的不同截口曲線可以是拋物線(齊曲線)、橢圓(虧曲線)和雙曲線(超曲線),並且研究了圓錐曲線的共軛直徑、切線和法線及其性質,也研究了圓錐曲線的極點和極線的性質。書中沒有談準線,但圓錐曲線是到定點(焦點)和到定直線(準線)的距離之比為常數(離心率)的點的軌跡,對此歐幾里得(Euclid)是知道的,並由帕普斯(Pappus,(A))述及且給出證明。這些對形成近代圓錐曲線的理論有著深遠的影響。自從笛卡兒(Descartes,R.)引進坐標系以來,沃利斯(Wallis,J.)在他的《論圓錐曲線》中,為了闡明阿波羅尼奧斯的結果,把幾何條件轉化為代數條件,第一個證明了動點坐標x,y的二元二次方程與幾何里的圓錐曲線對應,並開始用方程的理論來研究曲線的性質。16—17世紀,隨著機械工業的誕生和航海、建築、造船、採礦等事業的發達,推動了天文學和力學的發展。這時在天文學上發現行星的軌道是橢圓,力學上確定了拋射體的軌道是拋物線等,因此,有關圓錐曲線的深入研究也就成為迫切的需要了.到了18世紀,由於歐拉(Euler,L.)等多人的努力,圓錐曲線的現代理論才有了完美的結果。
曲線族
一組曲線,如果其中每一條曲線的方程都能夠從改變方程中所含的參數得到,就稱為一個曲線族,例如直線族等。微分方程通解的圖形,是一個曲線族。給參數以不同的值,就得到大小、位置或形狀不同的曲線。
曲線坐標
① 我國公元前一世紀成書的“周髀算經”內就已有“勾廣三,股修四,徑隅五”的記載。
對V的任一點y,有U的唯一的點 (u1,u2,…,un),其經f的象是y,該點叫做y的曲線坐標系。對U的任一點(a1,a2,…,an)及對[1,n]的任一元素j,設Uj為U與以Uj=aj為方程的仿射超平面的交。子流形Uj經f的象是A的超曲面,稱為坐標。
