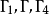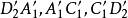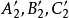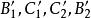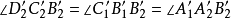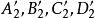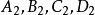六連環

六連環(six concatemer)亦稱古鏤錢，屬於平面幾何術語，指具有特殊位置關係的六個圓構成的圖形。設圓上有四點，通過第一、第二兩點，第二、第三兩點，第三、第四兩點，第四、第一兩點，各作一圓輪迴相交，則它們的四個第二交點共圓或共線。當四個交點共圓時，連同原來的圓及所作的四圓共六圓，我國從前把這圖形叫做六連環，也名古鏤錢。

基本介紹

• 中文名：六連環
• 外文名：six concatemer
• 所屬學科：數學
• 所屬問題：平面幾何(圓)
• 別名：古鏤錢
• 簡介：特殊位置關係的六個圓構成的圖形

基本介紹

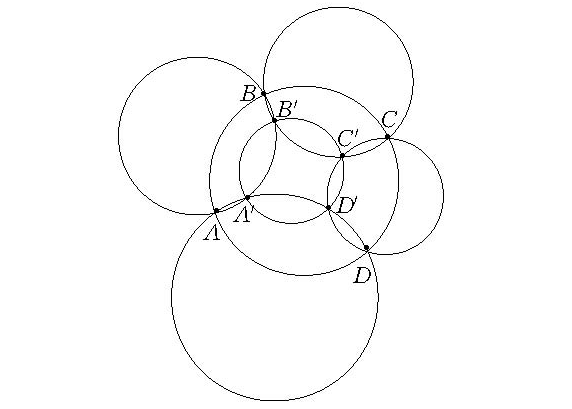
若A，B，C，D為定圓上的四個點，分別通過A和B，B和C，C和D，D和A各作一圓輪迴相交(如圖所示)，則所得另外四個交點A′，B′，C′，D′共圓或共線.當所得四交點共圓時，此圖形共有六個圓，稱此六個圓為六連環。

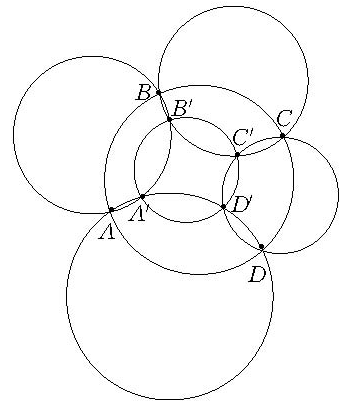圖1 六連環

若將其中圓改為定直線，命題仍直確，即：

定理 設定直線上有四點，通過其第一第二兩點，第二第三兩點，第三第四兩點，第四第一兩點，各作一圓輪迴相交，則所得四個第二交點共圓(圖2)或共線(圖3)。

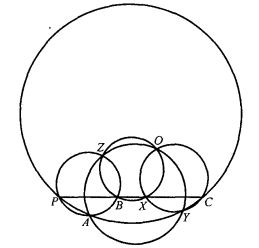圖2

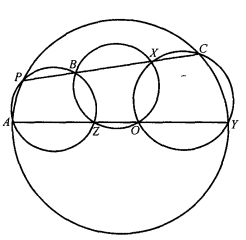圖3

六連環定理的證明

證明六連環定理：四圓循環相交，如果其中有四個交點共圓或共線，則另外四個交點也共圓或共線。

證明如圖4~7所示，設四個圓循環相交於點，且A₁、B₁、C₁、D₁四點在圓(直線)上。

以D₁為反演中心任作一反演變換，設點X的反點為X'，則的反形分別為直線，且分別在直線上，四點共圓，四點共圓(圖7)。於是有 ，因此，四點共圓，從而它們的反點四點共圓或共線。

六連環定理證明Miquel定理

利用六連環定理極易證明下面的Miquel定理。

五角星的五邊交成一個凸五邊形和五個三角形，則五個三角形的五個外接圓的異於五邊形的頂點的五個交點在一個圓上。

事實上，如圖8所示，設五角星的五個頂點分別為H、K、L、M、N，它的五邊交成凸五邊形ABCDE和五個三角形：△AHB、△BKC、△CLD、△DME、△ENA，這五個三角形的五個外接圓異於A、B、C、D、E的五個交點為P、Q、R、S、T，易知，點P、S都在△HLE的外接圓上，在⊙(AHB)、⊙(BKC)、⊙(CLD)、⊙(HLE)循環相交的八個交點中，有四個交點H、B、C、L共線，由六連環定理，另外四個交點P、Q、R、S共圓(不可能共線，因為P在∠NAH內，R在∠KCL內，S在∠LDM內，P、R、S三點不會共線)。同理，Q、R、S、T四點共圓，故P、Q、R、S、T五點共圓。

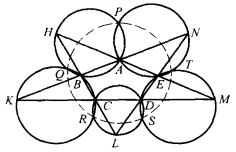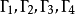
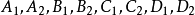
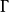
圖8