六角幻方指由正六邊型組成的幻方,理論上只有一種解法
基本介紹
- 中文名:六角幻方
- 外文名:Magic hexagon
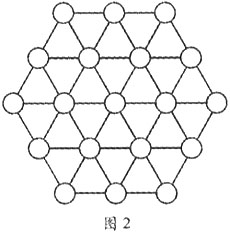
1910年,一位名叫阿當斯的鐵路公司閱覽室青年職員,對六角幻方很感興趣.他知道一層六角幻方(把1到7這7個數填入如圖1所示的圓圈內,使得任一條直線上的數字之和都等於同一個數)根本不存在,因而把注意力集中在由19個數組成的兩層六角幻方上.他一有空閒時間,便在紙上或地上畫兩層六角圖(如圖 2),再把19塊上面寫有1到19這19個數的硬紙板在圖上擺來擺去.就這樣,一天又一天,一年又一年,漫漫的47個春秋過去了,這時的阿當斯已不再是當年英俊瀟灑的小伙子,無情的歲月,使他成了兩鬢斑白的老人.面對無數次的失敗與挫折,阿當斯的興趣依然不減。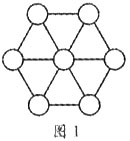


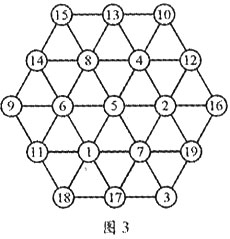
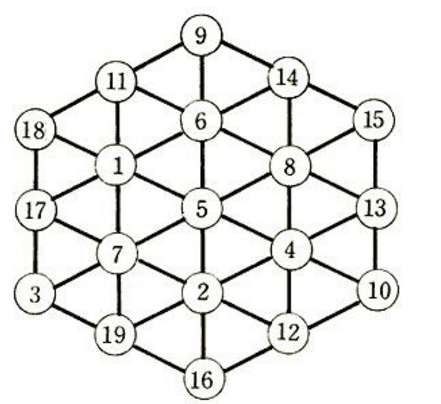
1957年的一天,患病在床的阿當斯終於排列成功了.他找連忙紙把它記錄下來,不幸的是,當他病癒出院回到家中時,卻發現那張記錄六角幻方的紙竟不見了。阿當斯並不因此灰心喪氣,又奮鬥了5年後,在1962年12月的一天,重新找到了那個丟失的圖形.這個圖形有個奇特的性質,就是橫的五行及斜的十行上各自數字的和都是38.
阿當斯對於耗費自己畢生心血而得來的六角幻方視如珍寶,並把它拿給幻方專家馬丁·加德納鑑賞.面對這巧奪天工的珍寶,馬丁·加德納博士頓感眼界大開,並為此寫信給智慧超群的數學遊戲專家特里格.特里格驚奇萬分並深受鼓舞,決心在阿當斯六角幻方的基礎上,對層數作出突破.他經過反覆研究,終於驚奇地發現:兩層以上的六角幻方根本不存在。這就是說,普通的幻方可能有千千萬萬種排法,但六角幻方卻只能有阿當斯這一個。