公切線定理

公切線是同時相切於兩條或兩條以上的曲線的直線。和兩個圓同時相切的直線叫做這兩個圓的公切線。

如果兩個圓在公切線的同側，則這公切線叫做這兩個圓的外公切線；如果兩個圓在公切線的異側，則這條直線叫做這兩個圓的內公切線。

圓的公切線有3個基本定理。

基本介紹

• 中文名：公切線定理
• 外文名：Common Tangent Theorem
• 學科：數學

定理定義

公切線是同時相切於兩條或兩條以上的曲線的直線。和兩個圓同時相切的直線叫做這兩個圓的公切線。

如果兩個圓在公切線的同側，則這公切線叫做這兩個圓的外公切線；如果兩個圓在公切線的異側，則這條直線叫做這兩個圓的內公切線。

一般地，兩圓公切線的長指的是該公切線上兩切點間的線段長度。

定理一

（1）外公切線的長=根號下圓心距的平方-大圓半徑減小圓半徑的平方

註：證明過程和圖示見圖冊。

　　

　　

　　

　　

（2）內公切線的長=根號下圓心距的平方-大圓半徑加小圓半徑的平方

註：證明過程和圖示見圖冊。

定理二

.外公切線與連心線夾角的正弦值=圓心距分之大圓半徑減小圓半徑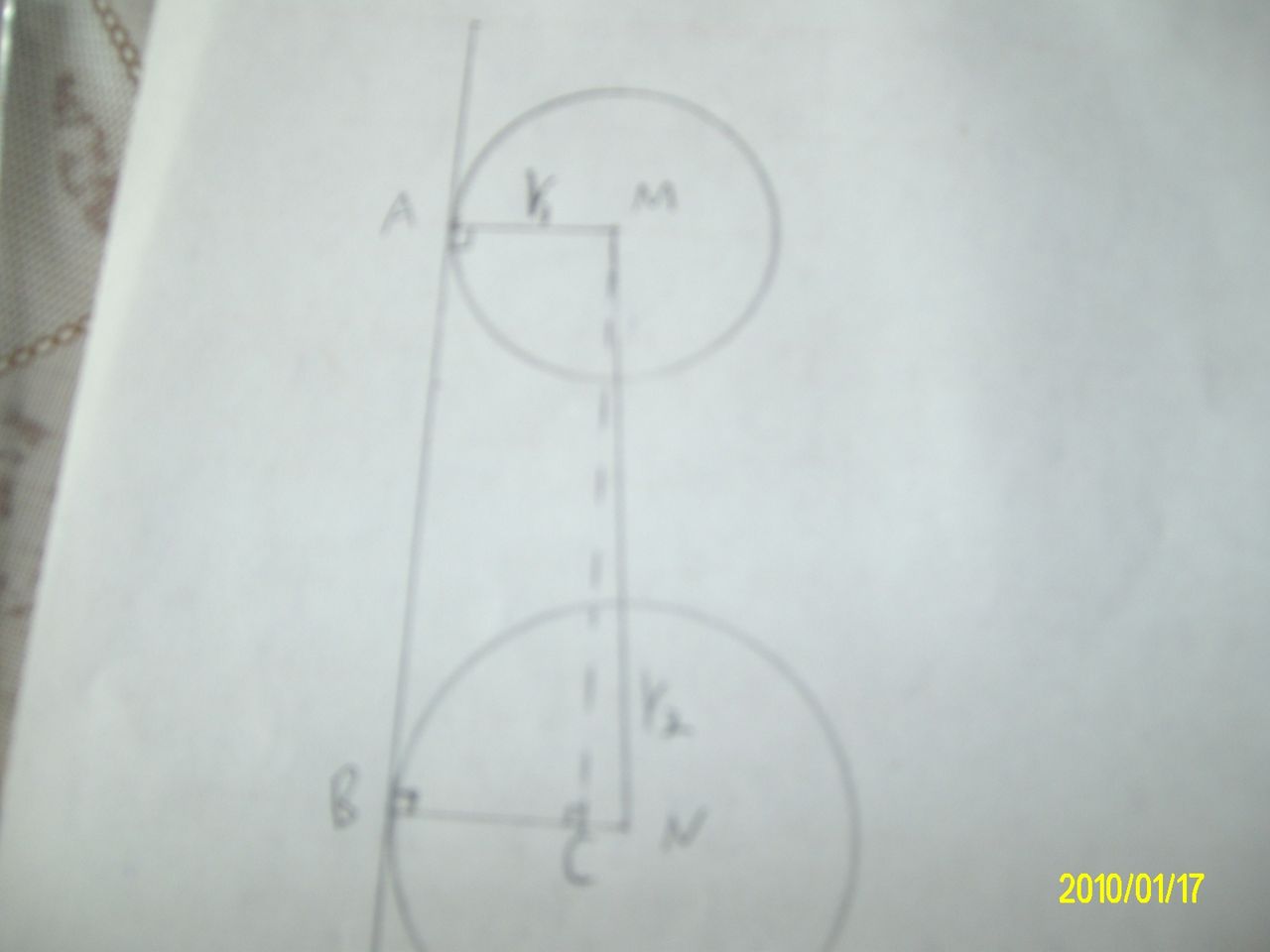

證明1圖

即：sin∠NMC=CN/MC=CN/AB

（可將NM與AB夾角平移至∠NMC）

證明略。

定理三

.內公切線與連心線夾角的正弦值=圓心距分之大圓半徑加小圓半徑

證明2圖

即sin∠MPA=（r1+r2）/MN

證明：在2.中已證明PM=(r1×MN)/(r1+r2)

∴sin∠MPA=MA/MP=r1/〔(r1×MN)/(r1+r2)〕=(r1+r2)/MN