全驅動系統是一類機械系統的統稱,其控制輸入數量等於被控制自由度的數量。在實際的物理模型中,存在大量的全驅動機械系統,具有操縱靈活、控制算法設計簡便的特點。
基本介紹
- 中文名:全驅動系統
- 外文名:Full actuated systems
- 所屬領域:系統與控制、機械工程
- 相關定義:欠驅動系統、過驅動系統
定義
牛頓形式下的描述


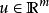


連線埠哈密頓的描述
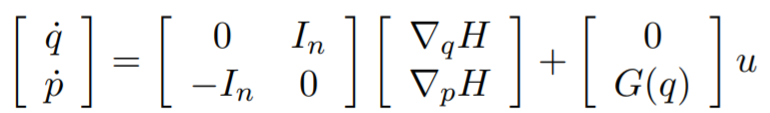





物理系統舉例
簡單機械臂
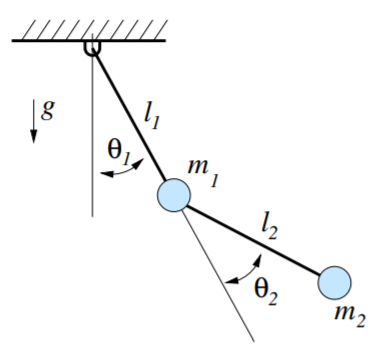

一些動力定位系統

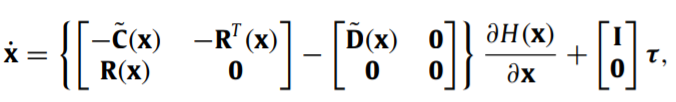

全驅動系統是一類機械系統的統稱,其控制輸入數量等於被控制自由度的數量。在實際的物理模型中,存在大量的全驅動機械系統,具有操縱靈活、控制算法設計簡便的特點。


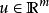


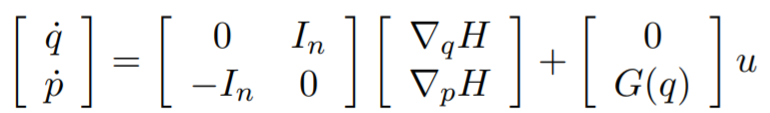








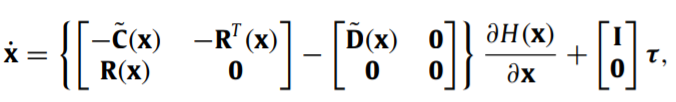
全驅動系統是一類機械系統的統稱,其控制輸入數量等於被控制自由度的數量。在實際的物理模型中,存在大量的全驅動機械系統,具有操縱靈活、控制算法設計簡便的特點。...
適時驅動介乎全時驅動和分時驅動之間,驅動模式由電腦安排,操縱非常簡單。採用這種驅動系統的車輛時根據電腦來控制並且選擇適合當下情況的驅動模式。在正常的路面上車輛...
驅動系統是電動汽車最主要的系統之一。電動汽車運行性能的好壞主要是由其驅動系統決定的。電動汽車驅動系統由牽引電機、電機控制器、機械傳動裝置、車輪等構成。它的...
非獨立式全電動空調系統壓縮機通過帶輪由驅動電動機帶動,結構相對簡單,此時壓縮機可以選擇傳統機械壓縮機,排量以及功率的選擇同機械式壓縮機。壓縮機運行工況的控制...
全時四驅系統,是指使汽車四個車輪一直保持有驅動力的四驅系統。...... 全時四驅系統(AWD)代表的汽車奧迪quartto系統 無論何時四個輪子都是屬於驅動力。使汽車四...
四輪驅動系統,又稱全輪驅動系統,是指汽車前後輪都有動力。可按行駛路面狀態不同而將發動機輸出扭矩按不同比例分布在前後所有的輪子上,以提高汽車的行駛能力。一般...
過驅動系統是一類控制輸入數多於輸出數的系統,冗餘控制為控制器的設計提供更大自由度的同時也提出挑戰。控制分配是處理冗餘控制的一種常用方法,同時對驅動器故障具有...
分時四驅(Part-time4WD):這是一種駕駛者可以在兩驅和四驅之間手動選擇的四輪驅動系統,由駕駛員根據路面情況,通過接通或斷開分動器來變化兩輪驅動或四輪驅動模式,這...
這是一種駕駛者可以在兩驅和四驅之間手動選擇的四輪驅動系統,由駕駛員根據路面情況,通過接通或斷開分動器來變化兩輪驅動或四輪驅動模式,這也是一般越野車或四驅SUV最...
這是一種駕駛者可以在兩驅和四驅之間手動選擇的四輪驅動系統,由駕駛員根據路面情況,通過接通或斷開分動器來變化兩輪驅動或四輪驅動模式,這也是一般越野車或四驅SUV最...
全輪驅動,又稱四輪驅動,是指汽車的總布置型式為全部車輪都是驅動輪。一般來說,發動機安裝在汽車的前部(也有的在汽車的中部),通過傳動系統帶動全部車輪驅動。全輪...
全時四輪驅動,簡稱AWD,是AllWheelDrive的簡寫。具體的含義是:汽車在行駛的任何時間,都是以四個輪子獨立推動,明顯區別於其他前輪或後輪以及4WD帶動的汽車。...
全輪驅動,是指汽車的總布置型式為全部車輪都是驅動輪。 ?nWD是全輪驅動(n Wheel Drive)的縮寫,n指與車輪總數相等的驅動輪數,我們在吉普車尾部時常能見到4WD的...
主軸驅動系統是數控工具機的大功率執行機構,其功能是接受數控系統(CNC)的S碼(速度指令)及M碼(輔助功能指令),驅動主軸進行切削加工。...
驅動程式一般指的是設備驅動程式(Device Driver),是一種可以使計算機和設備進行相互通信的特殊程式。相當於硬體的接口,操作系統只有通過這個接口,才能控制硬體設備的...
自動控制棒驅動系統是使控制棒上下運動或保持在某一高度的機構。主要類型有磁力提升式和磁阻馬達式。前者多用於陸上核電廠,後者多用於艦艇核動力裝置。它們都具有全...
傳動系統一般由離合器、變速器、萬向傳動裝置、主減速器、差速器和半軸等組成。其基本功用是將發動機發出的動力傳給汽車的驅動車輪,產生驅動力,使汽車能在一定速度...
尹建民,現任泛亞汽車技術中心有限公司驅動系統執行副總監。...... 尹建民,現任泛亞汽車技術中心有限公司驅動系統執行副總監。 [1] 尹建民人物榮譽 編輯 ...
十輪驅動(Ten-wheel drive)指傳動系統把引擎的動力同時傳送到十個車輪,這個設計主要在軍用車輛上使用 。相比掛接車輛,單一車體及全輪驅動的十輪車輛有較佳的...
1 詞語解釋 2 雲驅動傳統家電系統轉型 雲驅動詞語解釋 編輯 “雲驅動”功能使每位亞馬遜用戶可以免費將照片、音樂、文檔檔案、視頻上載到亞馬遜的伺服器上,然後方便...
全時四驅就是任何時間,車輛都是四個輪子獨立推動的驅動裝置。英文把"All Wheel Drive"簡寫"AWD",以有別於2WD(分FWD和RWD)。全時四驅通過一個柔性連線的中央...
xDrive智慧型全輪驅動系統 寶馬專利的xDrive在全輪驅動的靈敏性方面設立了新的標準。其工作就是迅速改變前後軸的扭力分布,提供真實的行車穩定性,駕駛樂趣以及安全性能。...
