內集合論是闡述非標準分析的一種公理方法。內集合論的公理系統從通常的ZFC公理系統出發,再加上一個新的一元謂詞“標準的”及轉換原理、理想化原理、標準化原理這三條公理構成。
基本介紹
- 中文名:內集合論
- 外文名:internal set theory
- 適用範圍:數理科學
簡介,公理,轉換原理,理想化原理,標準化原理,套用,
簡介
內集合論是闡述非標準分析的一種公理方法。
內集合論的公理系統從通常的ZFC公理系統出發,再加上一個新的一元謂詞“標準的”及轉換原理、理想化原理、標準化原理這三條公理構成。謂詞“標準的”指稱標準數學中,即通常數學中的具體對象。
公理
轉換原理
內集合論中的一個公式稱為內的,如果它不包含新的謂詞“標準的”,即它是ZFC中的一個公式,否則,這個公式就稱為外的。例如,“x 是標準的” 是一個最簡單的外公式,設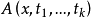 是一個內公式,
是一個內公式,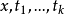 是自由變元,而且再無其他自由變元,則公式
是自由變元,而且再無其他自由變元,則公式
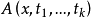
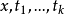
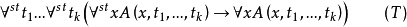
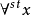
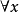
理想化原理
設 B(x,y) 是一個內公式,x,y 是自由變元,可能還有其他自由變元,則公式


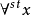
標準化原理
設C(z)是一個公式,它是內的或者是外單,z是自由變元,可能還有其他自由變元,則公式

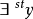
轉換原理(T)表示通常數學中的命題在內集合論中也成立。反之顯然也是對的。這正是非標準分析中的轉換原理。
理想化原理(I)表示任何一個共點的內二元關係在內集合論中可全滿足,這正是非標準分析中的飽和性。
標準化原理(S)是ZFC中的分離公理的補充,它表示對於任何一個標準集合r,存在一個標準子集y,y的標準元正好是x中滿足C的標準元。
內集合論的公理,即ZFC的公理加上(T),(S),(I),正好是非準分析的飽和模型中內集的基本性質。這也正是內集合論名稱的由來。
套用
若令B(x,y)表示實數集合上的二元關係:x<y,並且x,y>0,則(I)的左端顯然為真,即對任意標準的有限實數集z,存在一個小於z中每個實數y的實數x。由(I)其右端也為真,即存在一個大於零的實數r,對所有大於零的標準實數y,有x<y。換句話說,x是一個大於零的無限小。
類似地,若令B(x,y)表示實數集合上的關係:x>y,並且x,y>0,則由(I)可推出存在正無限大。有了非零無限小及無限大,在內集合論中就可展開非標準分析了。
這個方法已被法國非標準分析學派採用,並且在常微分方程的奇異攝動方面取得了很好的成果。
