克羅蒂-恩蓋塞定理

計算彈性體位移的一個定理，由義大利工程師F.克羅蒂於1878年和德國工程師F.恩蓋塞於1889年分別提出，因而得名。

基本介紹

• 中文名：克羅蒂－恩蓋塞定理
• 外文名：Crotti-Engesser's theorem
• 提出者：F.克羅蒂和F.恩蓋塞
• 提出時間：1878年和1889年

克羅蒂－恩蓋塞定理可敘述為：若彈性體上作用有n個已知的廣義力P₁，P₂，…，P_n，在它們的作用下沿每個廣義力方向的位移分別為δ₁，δ₂，…，δ_n，則由廣義力表示的余應變能U（見應變能）對某個廣義力Pi的偏導數等於與Pi相對應的廣義位移δi。其數學表達式為：

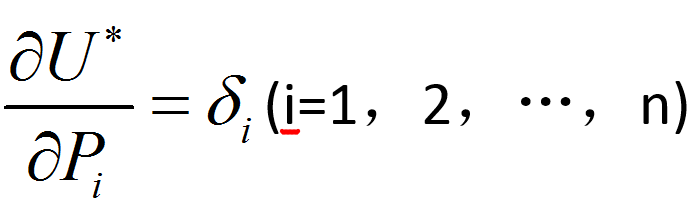
這一定理對線性或非線性體均適用。對於線性彈性體,應變能等於余應變能，而克羅蒂－恩蓋塞定理便成為卡氏第二定理：若線性彈性體作用有n個廣義外力P₁，P₂，…，P_n，在它們的作用下沿每個廣義外力方向的位移分別為δ₁，δ₂，…，δ_n，則由廣義力表示的應變能U對某個廣義力P_i的偏導數，就等於P_i與相對應的廣義位移δ_i。其數學表達式為：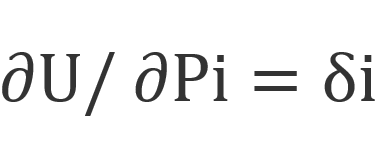

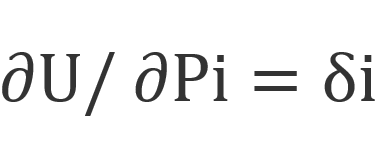
卡氏第二定理是義大利工程師A.卡斯蒂利亞諾於1873年提出的。它被用於求解彈性體的位移，也被用於求解靜不定結構問題。克羅蒂－恩蓋塞定理的價值還在於，由它可以直接導出結構分析中的兩個重要方法：力法和單位載荷法。