債券估價是為確定合理反映債券風險程度和收益能力的債券價格，而對債券未來收益作出的估算和評價。債券估價的基本問題是估算未來的現金收入。債券發行公司的財務實力(當前和長期)、資產價值、經營管理水平等相關資料都是在估價時需考慮的因素。為此，選擇反映上述情況的資料，據以對債券預期收益作出估計，並輔之以對未來變動因素的預測，是估價的基本手段。同時，估價時還要考察、權衡影響債券價值的外部力量，如市場利率的變化，稅收制度的特點，公共機構的需求和市場效率等。在一些情況下，這往往成為債券收益的決定因素。
基本介紹
- 中文名：債券估價
- 所屬領域：經濟
債券估價的基本方法
1、一般情況下的債券估價模型
典型的債券是固定利率、每年計算並支付利息、到期歸還本金。在此情況下，按複利方式計算的
債券價值的基本模型是：
公式
公式
式中：V——債券價值；
i——債券的票面利率；
F——到期的本金；
k——貼現率，一般採用當時的市場利率或投資人要求的最低報酬率；
n——債券到期前的年數。
【例1 】某公司擬2002年2月1日購買一張面額為1000元的債券，其票面利率為8%，每年2月
1日計算並支付一次利息，並於5年後的1月31日到期。當時的市場利率為10%，債券的市價是920元，應否購買該債券?
公式
=80 ×(P/A，10%，5)+1000 ×(P/S,10%,5)
=80 × 3.791+ 1000×0.621
=303.28+621
=924.28元＞920元
由於債券的價值大於市價，如不考慮風險問題，購買此債券是合算的。它可獲得大於10%的收益。
2、一次還本付息且不計算複利的債券估價模型
我國很多債券屬於一次還本付息且不計算複利的債券，其估價計算公式為：
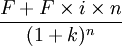
公式
【例2】某企業擬購買另一家企業發行的利隨本清的企業債券，該債券面值為1000元，期限為5年，票面利率為10%，不計複利，當前市場利率為8%，該債券的價格為多少時，企業才能購買?
由上述公式可知：
公式
即債券價格必須低於1020元時，企業才能購買。
3、折價發行時債券的估價模型
有些債券以折價方式發行，沒有票面利率，到期按面值償還。其估價模型為：
公式
公式中的符號含義同前式。
【例3】某債券面值為1000，期限為5年，以折現方式發行，期內不計利息，到期按面值償還，當時市場利率為8%，其價格為多少時，企業才能購買?
由上述公式可知：
V=1000×(P/S,8%,5)=1000×0.681=681元
即債券價格必須低於681元時，企業才能購買。
