偽相關

偽相關，這是統計學上的一個概念。實際上，在自然界裡存在兩種相關現象，除了真正的相關外,還有一種相關叫偽相關。太陽落山和月亮升起並沒有什麼因果關係，它只是地球自轉的反映,但這兩種現象確實是相關的,太陽落山的時候月亮正好升起，這就叫偽相關。

基本介紹

• 中文名：偽相關
• 外文名：spurious relationship
• 領域：統計學名詞
• 學科：數理科學
• 別稱：偽關係、虛假關係

簡介

偽相關(Spurious correlation)的定義最早由Karl Spearman提出，用以描述兩組由絕對測量值轉換而來的比例數據之間的相關，如百分比、千分比等。Spearman舉了一個簡單的例子：x, y, z為三組彼此間不相關的數據，但將前兩組數據與z相比後，將得出x/z與y/z中存在顯著相關（如圖1）。在另一張圖（圖2）中，我們以藍色和紅色分布標示較大或較小的分母z，會發現z較大的情況下，x/z與y/z較小，分布於左下，而較小的z對應著數值更大的x/z與y/z，可以說作為分母的z本身的影響，造成了x/z與y/z之間的線性分布，即使這三組數據間不存在任何關係。

在此我們了解到偽相關是指一種狹義的相關現象，而漢語民間語境中的偽相關，更多指的是另一統計術語“偽關係”。

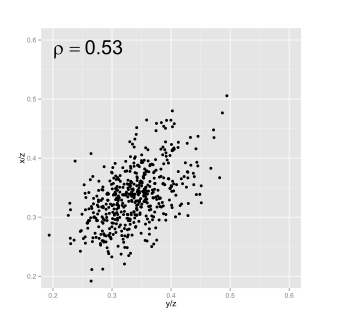圖1 相關性狀態圖

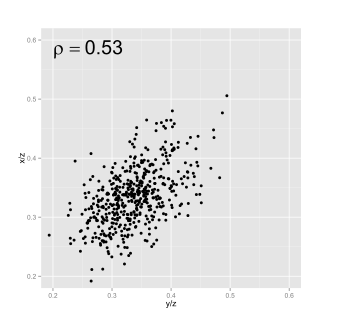圖2 相關性狀態圖

偽相關定義

偽相關(spurious relationship)，又稱偽關係、虛假關係，顧名思義是虛假的“關係”，但此處的關係指的是因果，而非相關，即兩因素間本不存在因果關係，卻被誤認為存在。這種錯誤出現的原因包括忽略了第三方潛在因素的影響，如前文介紹偽相關的例子，地球自轉對太陽落山與月亮上山的影響。嚴格意義上說，因為偽關係描述的是因果，如兩事物間的本身不被認為有因果關係，那也不會是偽關係。根據一些學者的說法，偽關係是相關向因果邁進的必經階段，排除了偽關係因素的相關研究才可能進一步探索因果關係。

對於偽關係的剔除目前主要有兩種方法：實驗與純統計檢驗。前者通過儘可能控制其它潛在影響因素，操縱其中某一變數並觀測另一變數的變化來明確兩者間的關係；後者則更多套用於一些無法付諸實驗而採用觀測數據的學科，如經濟學。

相關係數與偽相關

兩個變數可能會受第三者影響，從而在其間得出誤導性的相關係數。當變數 A 和 B 有相關時，有幾種可能：

1. A導致B；
   
2. B導致A；
   
3. C導致A和B。
   

第三種情況就會發生偽相關。如果在統計上控制住C變數，A和B就不再相關。

回歸現象與偽相關

當回歸分析中B隨A變化時，實際因果關係可能如下：

1. C → A → B；
   
2. A → C → B；
   
3. C → A；C → B。
   

示例

例一

統計研究發現，冰淇淋銷量最高的時候，就是公共泳池的溺水事故發生得最多的時候。

然而，有可能熱浪造成冰淇淋銷量和公共泳池的溺水事故增多。若視冰淇淋的銷量或遇溺事故為對方的成因，可能就被偽關係誤導了。

例二

荷蘭的統計數字顯示，在一連串的春季中，鸛鳥巢的數目與人類嬰兒出生數目之間呈現正相關。

兩者之間未必有因果關係。事實上，它們都和數據觀測之前9個月的天氣相關。

實驗

偽相關一詞常用於統計學上，特別是在實驗的測定結果上。實驗一般用以檢測如“X → Y”的因果關係。然而兩者的共同因素(W → X & Y)可造成非因果關係的相關。另外，如“X → W → Y”形的中介變數若沒有察覺出來的話，兩者非直接的關係便會看似是直接的。因此，除非能排除偽關係的可能性，否則實驗得出的相關並不代表因果關係。

實際上，下列三個條件都要成立，才可以得出X導致Y的結論：

• X發生在Y之前；
  
• 若X不發生則Y也不發生；
  
• 若X發生則Y一定發生。
  

如果上面三項中任何一項不符合，就可以確認出偽關係。

至於間接的因果關係，則不需要上列的第三項條件。例如，手槍決鬥中，兩個男人面對面，向對方開火。若其中一人擊中對方，而對方死亡，則可以推斷出他導致對方死亡。但是，若醫生把受傷的男人救回（不符合第三項條件），這沒有把因果關係終止，而只終止了直接的因果關係。由於開火X而導致身體受傷W，從而導致死亡Y。因為醫生的救治，終止了從W至Y的關係。