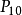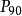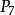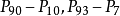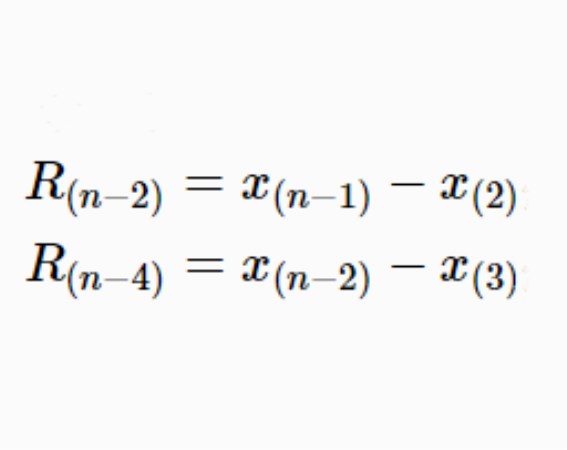修正極差是指剔除觀測值中極值後計算的極差。設順序統計量為X(1)≤X(2)≤…≤X(n),則剔除前後各一個極值後計算的極差稱為二級修正極差,即R2n=X(n-1)-X(2);剔除前後各二個極值後的三級修正極差為R3n=X(n-2)-X(3);依此類推,剔除前後各(m+1)個極值後的m級修正極差為Rmn=X(n-m+1)-X(m)。
基本介紹
- 中文名:修正極差
- 外文名:modified range
- 所屬學科:數學
- 簡介:剔除觀測值中極值後計算的極差
- 相關概念:極差,四分位差,百分位差等
基本介紹,四分位差,百分位差,
基本介紹
極差亦稱全距,是表示統計數據波動的最大幅度的散布特徵,等於統計數據中的最大值與最小值之差。對於任意一組數據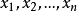 ,其各觀測值按從小到大的順序排列,得
,其各觀測值按從小到大的順序排列,得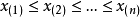 ,最大觀測值
,最大觀測值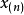 和最小觀測值
和最小觀測值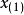 之差稱為極差,記作Rn,即
之差稱為極差,記作Rn,即
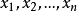
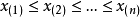
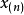
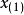
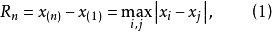
極差只考慮了數據中最大值與最小值,而沒有涉及數據中的其他值。極差的計算簡單易行,便於理解,但是,由於極差忽略了其餘觀察值之間的本來差異,所以只能粗略地反映統計數據的分布程度,兩組數據極差相等,其散布情況卻可能相差甚遠,另外,由於數據的最大值和最小值受異常偶然因素影響的可能性最大,所以級差極易受異常值影響。
修正極差 為了消除可能出現的異常值的影響,有時使用修正極差(modified range)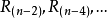 ,其中,
,其中,
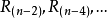
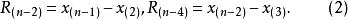
四分位差
四分位差是用第一四分位數和第三四分位數差的一半作為差異量數。
四分位差用QD來表示。
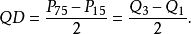
四分位差比較能反映出分布數據中間的散布情況,但由於它忽略了上下各25%數據的情況。所以它的缺點是保了中間,丟了兩頭,對我們全面了解數據的情況帶來了一定的困擾。
百分位差
百分位差(percentile deviation)是也一種差異量數,百分位差是用百分位數之間的差距來描述離中趨勢的一種差異量。
用百分位數的差距作為差異量通常有兩種:一是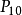 到
到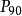 ;二是
;二是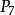 到
到 。前者包括了中間80%個數據,後者包括了86%的數據。計算公式分別為:
。前者包括了中間80%個數據,後者包括了86%的數據。計算公式分別為: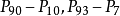 。但這兩種百分位差,雖然比全距較少受兩極數據的影響,但仍然不能很好地反映中間數據的散布情況,因此只作為主要差異量數的補助量數。
。但這兩種百分位差,雖然比全距較少受兩極數據的影響,但仍然不能很好地反映中間數據的散布情況,因此只作為主要差異量數的補助量數。