保測變換共軛(conjugacy of measure-pre-serving transformations)是保測變換分類的一種方法。
基本介紹
- 中文名:保測變換共軛
- 外文名:conjugacy of measure-pre-serving transformations
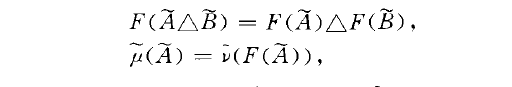

保測變換共軛(conjugacy of measure-pre-serving transformations)是保測變換分類的一種方法。
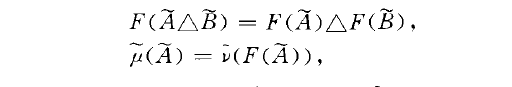
保測變換共軛(conjugacy of measure-pre-serving transformations)是保測變換分類的一種方法。設(X,,,川為機率空間,在了上引人等價關係:A一B(AB)一o CbA,BE.-...
《遍歷理論引論》是2022年哈爾濱工業大學出版社出版的圖書。內容簡介 本書是動力系統遍歷理論的代表作,共分為11章,它們的內容分別是:預備知識,保測變換,自同構、共軛與譜同構,具有離散譜的保測變換,熵,拓撲動力學,連續變換的不變測度,拓撲熵,拓撲熵與測度論熵之間的關係,拓撲壓力和它與不變測度的關係,...
是同構的,對保測系統 ,令 設 分別為 上的保測變換,若存在同構 ,使 ,則稱T和S是共軛的。容易證明,同構⇒共軛⇒譜同構,但反之未必成立。在一定條件下,例如,當X,Y為完備可分度量空間,為波萊爾機率空間時,同構與共軛是等價的。其他介紹 定義 設 為機率空間,在 上定義等價關係:稱A和B...
《實分析與泛函分析》共分為13章,內容包括實變泛函的基本內容,如度量空間、測度和測度的擴張、可測函式、Banach空間的幾個基本定理,共軛空間與共軛運算元,Hilbert空間上有界線性運算元的譜分解,遍歷定理與保測變換的遍歷性等。另外還補充了一些對於擴大視野和進一步深入研究很有意義的內容,如套用Baire定理給出處處不...
亞純函式周期點的存在性,給出恰當周期點個數的定量估計;雙曲區域上的自映照與Mobius變換的共軛問題;各類周期域與遊蕩域的特性和存在性; [1],如 Julia集的分布、單點分支和淹沒分支的存在性、一致完全性以及Lebesgue測度等;亞純函式族的穩定性和結構穩定性;Julia集的Hausdorff維數,尤其是具有代表性的幾類亞純函式...
